Câu hỏi
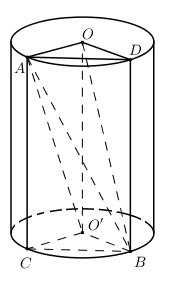
Cho hình trụ có đáy là hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R} \right)\), chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm \(O\) lấy điểm \(A\), trên đường tròn đáy tâm \(O'\) lấy điểm \(B\). Thể tích của khối tứ diện\(OO'AB\) có giá trị lớn nhất bằng:
- A \(\dfrac{{{R^3}}}{2}\)
- B \(\dfrac{{\sqrt 3 {R^3}}}{3}\)
- C \(\dfrac{{{R^3}}}{6}\)
- D \(\dfrac{{{R^3}}}{3}\)
Phương pháp giải:
+) Gọi \(C\) là hình chiếu của \(A\) lên mặt đáy chứa đường tròn \(\left( {O';R} \right)\) và \(D\) là hình chiếu của \(B\) lên mặt đáy chứa đường tròn \(\left( {O;R} \right)\).
+) Tính thể tích lăng trụ đứng \(OAD.O'CB\), từ đó suy ra thể tích tứ diện\(OO'AB\) và đánh giá.
Lời giải chi tiết:
Gọi \(C\) là hình chiếu của \(A\) lên mặt đáy chứa đường tròn \(\left( {O';R} \right)\) và \(D\) là hình chiếu của \(B\) lên mặt đáy chứa đường tròn \(\left( {O;R} \right)\).
Khi đó ta có lăng trụ đứng \(OAD.O'CB\).
Ta có
\(\begin{array}{l}{V_{OO'AB}} = {V_{OAD.O'CB}} - {V_{A.O'BC}} - {V_{O'.OAD}} = {V_{OAD.O'CB}} - \dfrac{1}{3}{V_{OAD.O'CB}} - \dfrac{1}{3}{V_{OAD.O'CB}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}{V_{OAD.O'CB}} = \dfrac{1}{3}AC.{S_{OAD}} = \dfrac{1}{3}.AC.\dfrac{1}{2}OA.OD.\sin \angle AOD\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}.2R.{R^2}.\sin \angle AOD = \dfrac{{{R^3}}}{3}\sin \angle AOD\end{array}\)
\( \Rightarrow \max {V_{OO'AB}} = \dfrac{{{R^3}}}{3} \Leftrightarrow \sin \angle AOD = 1 \Leftrightarrow OA \bot OD \Leftrightarrow OA \bot O'B\).
Chọn D.