Phương pháp giải:

+) Gắn hệ trục tọa độ.

+) Viết phương trình đường thẳng \(\Delta \) là trục của \(\Delta CMN\).

+) Viết phương trình mặt phẳng trung trực \(\left( P \right)\) của \(SC.\)

+) Tâm mặt cầu ngoại tiếp chóp \(S.CMN\) là \(I = \left( P \right) \cap \Delta \).

+) Tính \(R = IS = IC = IM = IN\).

Lời giải chi tiết:

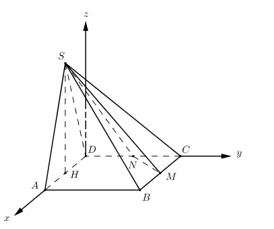
Gọi \(H\) là trung điểm của \(AD \Rightarrow SH \bot AD \Rightarrow SH \bot \left( {ABCD} \right)\).

Gắn hệ trục tọa độ như hình vẽ. Chọn \(a = 1\).

Ta có: \(D\left( {0;0;0} \right),\,\,A\left( {1;0;0} \right),\,\,B\left( {1;1;0} \right),\,\,C\left( {0;1;0} \right),\,\,S\left( {\dfrac{1}{2};0;\dfrac{{\sqrt 3 }}{2}} \right)\)

\(M\left( {\dfrac{1}{2};1;0} \right),\,\,N\left( {0;\dfrac{1}{2};0} \right)\).

Gọi \(E\left( {\dfrac{1}{4};\dfrac{3}{4};0} \right)\) là trung điểm của \(MN\).

Tam giác \(CMN\) vuông tại \(C \Rightarrow E\) là tâm đường tròn ngoại tiếp \(\Delta CMN\).

Gọi \(\Delta \) là đường thẳng qua \(E\) và vuông góc với \(\left( {ABCD} \right)\) \( \Rightarrow \Delta \) nhận \(\overrightarrow k  = \left( {0;0;1} \right)\) là VTCP \( \Rightarrow \Delta :\,\,\left\{ \begin{array}{l}x = \dfrac{1}{4}\\y = \dfrac{3}{4}\\z = t\end{array} \right.\).

Gọi \(K\left( {\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{4}} \right)\) là trung điểm của \(SC\).

Ta có \(\overrightarrow {SC}  = \left( { - \dfrac{1}{2};1; - \dfrac{{\sqrt 3 }}{2}} \right)//\left( {1; - 2;\sqrt 3 } \right)\).

\( \Rightarrow \) Mặt phẳng trung trực của SC đi qua \(K\) và nhận \(\left( {1; - 2;\sqrt 3 } \right)\) là 1 VTPT có phương trình:

\(1\left( {x - \dfrac{1}{4}} \right) - 2\left( {y - \dfrac{1}{2}} \right) + \sqrt 3 \left( {z - \dfrac{{\sqrt 3 }}{4}} \right) = 0 \Leftrightarrow x - 2y + \sqrt 3 z = 0\,\,\left( P \right)\)

Gọi \(I = \left( P \right) \cap \Delta  \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.CMN\).

\(\begin{array}{l}I \in \Delta  \Rightarrow I\left( {\dfrac{1}{4};\dfrac{3}{4};t} \right)\\I \in \left( P \right) \Rightarrow \dfrac{1}{4} - \dfrac{3}{2} + \sqrt 3 t = 0 \Leftrightarrow t = \dfrac{{5\sqrt 3 }}{{12}} \Rightarrow I\left( {\dfrac{1}{4};\dfrac{3}{4};\dfrac{{5\sqrt 3 }}{{12}}} \right)\\ \Rightarrow R = IC = \sqrt {\dfrac{1}{{16}} + \dfrac{1}{{16}} + \dfrac{{25}}{{48}}}  = \dfrac{{\sqrt {93} }}{{12}}.\end{array}\)   

Chọn A.