Câu hỏi
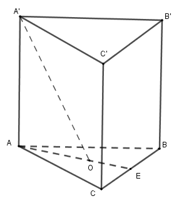
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(2a,\) \(O\) là trọng tâm tam giác \(ABC\) và \(A'O = \dfrac{{2a\sqrt 6 }}{3}.\) Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
- A \(2{a^3}.\)
- B \(2{a^3}\sqrt 3 .\)
- C \(\dfrac{{4{a^3}}}{3}.\)
- D \(\dfrac{{2{a^3}}}{3}.\)
Phương pháp giải:
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ \(V = S.h\) với \(S\) là diện tích đáy và \(h\) là chiều cao lăng trụ
Lời giải chi tiết:
Gọi \(E\) là trung điểm của \(BC.\)
Vì \(ABC\) là tam giác đều cạnh \(2a\) nên \(AE = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
Vì \(O\) là trọng tâm tam giác \(ABC\) nên \(AO = \dfrac{2}{3}.AE = \dfrac{2}{3}.a\sqrt 3 = \dfrac{{2a\sqrt 3 }}{3}\)
Xét tam giác \(AOA'\) vuông tại \(A\) nên \(AA' = \sqrt {A'{O^2} - A{O^2}} = \sqrt {{{\left( {\dfrac{{2a\sqrt 6 }}{3}} \right)}^2} - {{\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{2a\sqrt 3 }}{3}\)
Diện tích đáy \({S_{ABC}} = \dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Thể tích lăng trụ \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = \dfrac{{2a\sqrt 3 }}{3}.{a^2}\sqrt 3 = 2{a^3}.\)
Chọn A.