Phương pháp giải:

Hàm số \(y = f\left( x \right)\)  đồng biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\;\;\forall x \in \left( {a;\;b} \right).\)

Lời giải chi tiết:

Hàm số \(f\left( x \right)\) đồng biến  \( \Leftrightarrow f'\left( x \right) \ge 0 \Leftrightarrow \left( {x - 2} \right)\left( {x + 5} \right)\left( {x + 1} \right) \ge 0\)

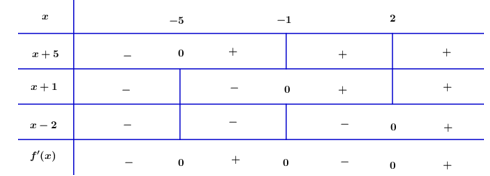
Ta có bảng xét dấu:

\( \Rightarrow f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 5 < x <  - 1\\x > 2\end{array} \right..\)

Chọn A.