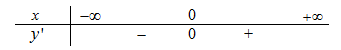Phương pháp giải:

Hàm số \(y = f\left( x \right)\)  đồng biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\;\;\forall x \in \left( {a;\;b} \right).\)

Lời giải chi tiết:

Ta có: \(y' = 4{m^2}{x^3} - 4\left( {4m - 1} \right)x\)

+) Xét \(m = 0 \Rightarrow y' = 4x > 0\,\,\forall x \in \left( {1; + \infty } \right) \Rightarrow \)  Hàm số đã cho đồng biến trên \(\left( {1; + \infty } \right) \Rightarrow m = 0\) thỏa mãn bài toán.

+) Xét \(m \ne 0 \Rightarrow y' = 0\,\, \Leftrightarrow 4{m^2}{x^3} - 4\left( {4m - 1} \right)x = 0\,\,\, \Leftrightarrow 4x\left( {{m^2}{x^2} - 4m + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = \dfrac{{4m - 1}}{{{m^2}}}\,\,\,\left( 1 \right)\end{array} \right.\)

BXD:

\( \Rightarrow \) Hàm số đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow \) Hàm số đồng biến trên \(\left( {1; + \infty } \right)\) \( \Rightarrow m \le \dfrac{1}{4}\,\,tm\).

Giả sử \({x_1} < {x_2}\) là 2 nghiệm phân biệt của phương trình (1) khi đó ta có bảng biến thiên:

Dựa vào BBT ta thấy để hàm số đồng biến trên \(\left( {1; + \infty } \right) \Rightarrow {x_1} < {x_2} \le 1 \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} < 2\\\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) \ge 0\end{array} \right.\).

Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 0\\{x_1}{x_2} = \dfrac{{ - 4m + 1}}{{{m^2}}}\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}0 < 2\,\,\left( {luon\,\,dung} \right)\\\dfrac{{ - 4m + 1}}{{{m^2}}} + 1 \ge 0\end{array} \right. \Leftrightarrow \dfrac{{{m^2} - 4m + 1}}{{{m^2}}} \ge 0 \Leftrightarrow {m^2} - 4m + 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}m \ge 2 + \sqrt 3 \\m \le 2 - \sqrt 3 \end{array} \right.\).

Kết hợp điều kiện \( \Rightarrow m \in \left( {\dfrac{1}{4};2 - \sqrt 3 } \right] \cup \left[ {2 + \sqrt 3 ; + \infty } \right)\).

Kết hợp các trường hợp ta có \(m \in \left( { - \infty ;2 - \sqrt 3 } \right] \cup \left[ {2 + \sqrt 3 ; + \infty } \right)\).

Kết hợp điều kiện đề bài ta có \(\left\{ \begin{array}{l}m \in \left( { - 10;2 - \sqrt 3 } \right] \cup \left[ {2 + \sqrt 3 ;10} \right)\\m \in \mathbb{Z}\end{array} \right. \Rightarrow m \in \left\{ { - 9; - 8;...;0;4;5;...;9} \right\} \Rightarrow \) Có 16 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn B.