Câu hỏi
Cho khối nón \(\left( N \right)\) đỉnh \(S\), có chiều cao là \(a\sqrt 3 \) và độ dài đường sinh là \(3a\). Mặt phẳng \(\left( P \right)\) đi qua đỉnh \(S\), cắt và tạo với mặt đáy của khối nón một góc \({60^0}\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( P \right)\) và khối nón \(\left( N \right)\).
- A \(2{a^2}\sqrt 5 \)
- B \({a^2}\sqrt 3 \)
- C \(2{a^2}\sqrt 3 \)
- D \({a^2}\sqrt 5 \)
Phương pháp giải:
Xác định góc giữa hai mặt phẳng và tính toán dựa vào các kiến thức hình học đã biết.
Lời giải chi tiết:
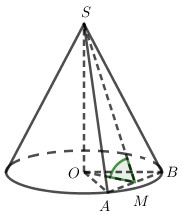
Gọi \(M\) là trung điểm của \(AB\) thì \(SM \bot AB,OM \bot AB\) \( \Rightarrow \) góc giữa \(\left( {SAB} \right)\) với mặt đáy bằng góc giữa \(SM\) và \(OM\) hay \(\widehat {SMO} = {60^0}\).
Tam giác \(SOM\) vuông tại \(O\) có \(SO = a\sqrt 3 ,\,\,\widehat {SMO} = {60^0} \Rightarrow SM = \dfrac{{SO}}{{\sin {{60}^0}}} = a\sqrt 3 :\dfrac{{\sqrt 3 }}{2} = 2a\).
Lại có, tam giác \(SMA\) vuông tại \(M\) có \(MA = \sqrt {S{A^2} - S{M^2}} = \sqrt {9{a^2} - 4{a^2}} = a\sqrt 5 \Rightarrow AB = 2MA = 2a\sqrt 5 \).
Vậy diện tích \({S_{SAB}} = \dfrac{1}{2}SM.AB = \dfrac{1}{2}.2a.2a\sqrt 5 = 2{a^2}\sqrt 5 \).
Chọn A.







