Câu hỏi
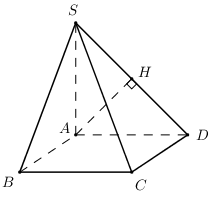
Cho hình chóp \(S.ABCD,\) đáy\(ABCD\)là hình chữ nhật có \(AB = a,{\rm{ }}AD = 2a;{\rm{ }}SA\) vuông góc với đáy, khoảng cách từ \(A\) tới \(\left( {SCD} \right)\) bằng \(\dfrac{a}{2}\). Tính thể tích khối chóp theo \(a\) .
- A \(\dfrac{{2\sqrt 5 }}{{15}}{a^3}.\)
- B \(\dfrac{{2\sqrt 5 }}{{45}}{a^3}.\)
- C \(\dfrac{{4\sqrt {15} }}{{15}}{a^3}.\)
- D \(\dfrac{{4\sqrt {15} }}{{45}}{a^3}.\)
Phương pháp giải:
+) Kẻ \(AH \bot SD\), chứng minh \(AH \bot \left( {SCD} \right)\).
+) \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}}\).
Lời giải chi tiết:
Trong \(\left( {SAD} \right)\) kẻ \(AH \bot SD\,\,\left( {H \in SD} \right)\).
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\,\,\left( {gt} \right)\\CD \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\\\left\{ \begin{array}{l}AH \bot SD\\AH \bot CD\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right) \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH\end{array}\)
Xét tam giác vuông \(SAD\):
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}} \Leftrightarrow \dfrac{4}{{{a^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{4{a^2}}} \Leftrightarrow SA = \dfrac{{2a}}{{\sqrt {15} }}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}.SA.AD.AD = \dfrac{1}{3}.\dfrac{{2a}}{{\sqrt {15} }}.a.2a = \dfrac{{4\sqrt {15} }}{{45}}{a^3}\)
Chọn D.