Câu hỏi
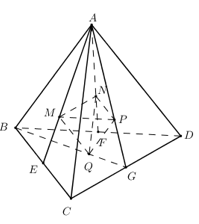
Cho khối tứ diện \(ABCD\) có thể tích là \(V\). Gọi \(E,\,\,F,\,\,G\) lần lượt là trung điểm \(BC,\,\,BD,\,\,CD\) và \(M,\,\,N,\,\,P,\,\,Q\) lần lượt là trọng tâm \(\Delta ABC,\,\,\Delta ABD,\,\,\Delta ACD,\,\,\Delta BCD\). Tính thể tích khối tứ diện \(MNPQ\) theo \(V\).
- A \(\dfrac{V}{9}\)
- B \(\dfrac{V}{3}\)
- C \(\dfrac{{2V}}{9}\)
- D \(\dfrac{V}{{27}}\)
Phương pháp giải:
So sánh tỉ số chiều cao và tỉ số diện tích đáy, từ đó suy ra tỉ số thể tích.
Lời giải chi tiết:
Ta có: \(\dfrac{{AM}}{{AE}} = \dfrac{{AP}}{{AG}} = \dfrac{{AN}}{{AF}} = \dfrac{2}{3} \Rightarrow MP//EG,\,\,MN//EF\)
\( \Rightarrow \left( {MNP} \right)//\left( {BCD} \right)\).
Ta có \(\dfrac{{MN}}{{EG}} = \dfrac{2}{3} \Rightarrow \dfrac{{MN}}{{BD}} = \dfrac{1}{3}\)
Ta có \(\Delta MNP\) đồng dạng với \(\Delta BCD\) theo tỉ số \(\dfrac{1}{3} \Rightarrow \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta BCD}}}} = \dfrac{1}{9}\).
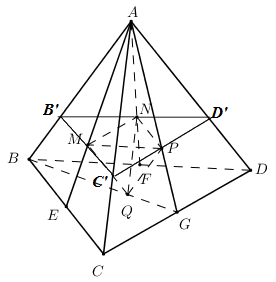
Dựng \(B'C'\) qua M và song song \(BC\). \(C'D'\) qua P và song song với \(CD\).
\( \Rightarrow \left( {MNP} \right) \equiv \left( {B'C'D'} \right)\).
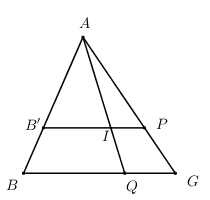
Trong \(\left( {ABG} \right)\) gọi \(I = AQ \cap B'P\). Ta có \(\dfrac{{AB'}}{{AB}} = \dfrac{{AI}}{{AQ}} = \dfrac{{AP}}{{AG}} = \dfrac{2}{3}\).
\(\begin{array}{l}\dfrac{{d\left( {Q;\left( {MNP} \right)} \right)}}{{d\left( {A;\left( {MNP} \right)} \right)}} = \dfrac{{QI}}{{AI}} = \dfrac{1}{2};\,\,\dfrac{{d\left( {A;\left( {MNP} \right)} \right)}}{{d\left( {A;\left( {BCD} \right)} \right)}} = \dfrac{{AB'}}{{AB}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{d\left( {Q;\left( {MNP} \right)} \right)}}{{d\left( {A;\left( {BCD} \right)} \right)}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\end{array}\)
Vậy \(\dfrac{{{V_{MNPQ}}}}{{{V_{ABCD}}}} = \dfrac{1}{3}.\dfrac{1}{9} = \dfrac{1}{{27}} \Rightarrow {V_{MNPQ}} = \dfrac{V}{{27}}\).
Chọn D.