Câu hỏi
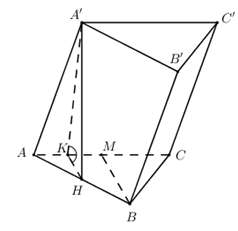
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu vuông góc của \(A'\) xuống \(\left( {ABC} \right)\) là trung điểm của \(AB\). Mặt bên \(\left( {ACC'A'} \right)\) tạo với đáy góc \({45^o}\). Tính thể tích khối lăng trụ \(ABC.A'B'C'\).
- A \(\dfrac{{3{a^3}}}{{16}}\).
- B \(\dfrac{{{a^3}\sqrt 3 }}{3}\).
- C \(\dfrac{{2{a^3}\sqrt 3 }}{3}\).
- D \(\dfrac{{{a^3}}}{{16}}\).
Phương pháp giải:
+) Gọi \(M\) là trung điểm của \(AC\). Gọi \(K\) là trung điểm của \(AM\), chứng minh \(\angle \left( {\left( {ACC'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {A'K;KH} \right)\)
Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AC \Rightarrow BM \bot AC\).
Gọi \(K\) là trung điểm của \(AM\). Ta có \(KH\) là đường trung bình của tam giacx \(ABM\)
\( \Rightarrow KH//BM \Rightarrow KH \bot AC\) và \(KH = \dfrac{1}{2}BM = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\).
Ta có: \(\left\{ \begin{array}{l}AC \bot A'H\,\,\left( {gt} \right)\\AC \bot KH\end{array} \right. \Rightarrow AC \bot \left( {AKH} \right) \Rightarrow C \bot A'K\)
\(\begin{array}{l}\left\{ \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {ABC} \right) = AC\\\left( {ACC'A'} \right) \supset A'K \bot AC\\\left( {ABC} \right) \supset KH \bot AC\end{array} \right.\\ \Rightarrow \angle \left( {\left( {ACC'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {A'K;KH} \right) = \angle A'KH = {45^0}\end{array}\)
\( \Rightarrow \Delta A'KH\) vuông cân tại \(H \Rightarrow A'H = KH = \dfrac{{a\sqrt 3 }}{4}\).
\( \Rightarrow {V_{ABC.A'B'C'}} = A'H.{S_{\Delta ABC}} = \dfrac{{a\sqrt 3 }}{4}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}}}{{16}}\).
Chọn A.