Câu hỏi
Một khối trụ bán kính đáy là \(a\sqrt 3 ,\) chiều cao là \(2a\sqrt 3 .\) Tính thể tích khối cầu ngoại tiếp khối trụ.
- A \(8\sqrt 6 \pi {a^3}\)
- B \(6\sqrt 6 \pi {a^3}\)
- C \(4\sqrt 3 \pi {a^3}\)
- D \(\dfrac{{4\sqrt 6 }}{3}\pi {a^3}\)
Phương pháp giải:
Công thức tính thể tích khối cầu bán kính \(R:\,\,V = \dfrac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
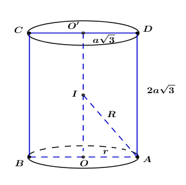
Gọi \(I\) là trung điểm của \(OO'.\)
\( \Rightarrow I\) là tâm mặt cầu ngoại tiếp khối trụ.
\(\begin{array}{l} \Rightarrow R = \sqrt {I{O^2} + O{A^2}} = \sqrt {3{a^2} + 3{a^2}} = a\sqrt 6 .\\ \Rightarrow V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {a\sqrt 6 } \right)^3} = 8\sqrt 6 \pi {a^3}.\end{array}\)
Chọn A.
Câu hỏi trước
