Câu hỏi
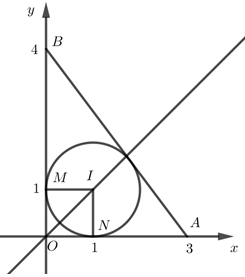
Trên mặt phẳng tọa độ \(Oxy,\) cho các điểm \(A\left( {3;0} \right)\) và \(B\left( {0;4} \right)\). Đường tròn nội tiếp tam giác \(OAB\) có phương trình là:
- A \({x^2} + {y^2} = 1\)
- B \({x^2} + {y^2} - 4x + 4 = 0\)
- C \({x^2} + {y^2} = 2\)
- D \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\)
Phương pháp giải:
Gọi I là tâm đường tròn nội tiếp \(\Delta OAB\) mà A, B lần lượt nằm trên Ox, Oy nên phân giác góc AOB chính là phân giác góc phần tư thứ I và III có phương trình: \(y = x\). Gọi tọa độ của điểm I theo một chữ.
Lập phương trình theo khoảng cách \(d\left( {I;OA} \right) = d\left( {I;AB} \right)\) để tìm I từ đó loại đáp án.
Lời giải chi tiết:
Gọi I là tâm đường tròn nội tiếp mà A, B lần lượt nằm trên Ox, Oy nên phân giác góc AOB chính là phân giác góc phần tư thứ I và III có phương trình: \(y = x\)
Phương trình đường thẳng \(AB:\,\,\frac{x}{3} + \frac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0.\)
Phương trình \(OA:\,\,x = 0.\)
Gọi \(I\left( {m;m} \right)\,\,\left( {m < 3} \right)\) là tâm đường tròn nội tiếp ta có:
\(\begin{array}{l}\,\,\,\,\,\,d\left( {I;OA} \right) = d\left( {I;AB} \right) \Leftrightarrow \left| m \right| = \frac{{\left| {7m - 12} \right|}}{5}\\ \Leftrightarrow \left| {7m - 12} \right| = 5\left| m \right| \Leftrightarrow \left[ \begin{array}{l}7m - 12 = 5m\\12 - 7m = 5m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 6\,\,\left( {ktm} \right)\\m = 1\,\,\,\left( {tm} \right)\end{array} \right..\end{array}\)
Vậy \(I\left( {1;1} \right)\) là tâm đường tròn nội tiếp của
Phương trình đường tròn cần tìm: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1.\)
Chọn D.