Câu hỏi
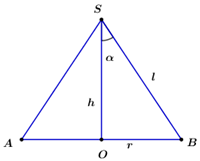
Cho hình nón tròn xoay có bán kính đáy bằng \(3\) và diện tích xung quanh bằng \(6\sqrt 3 \pi \) . Góc ở đỉnh của hình nón đã cho bằng
- A \({60^0}\)
- B \({150^0}\)
- C \({90^0}\)
- D \({120^0}\)
Phương pháp giải:
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(R,\;\) chiều cao \(h\) và đường sinh \(l:\;\;{S_{xq}} = \pi Rl.\)
Lời giải chi tiết:
Ta có: \(R = 3.\)
\( \Rightarrow {S_{xq}} = \pi Rl \Leftrightarrow \pi .3.l = 6\pi \sqrt 3 \Leftrightarrow l = 2\sqrt 3 .\)
\(\begin{array}{l} \Rightarrow \sin \alpha = \frac{R}{l} = \frac{3}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{2}\\ \Rightarrow \alpha = {60^0} \Rightarrow \angle ASB = {2.60^0} = {120^0}.\end{array}\)
Chọn D.