Phương pháp giải:

Diện tích tam giác: \(S = pr = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)

Lời giải chi tiết:

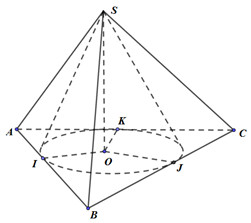
Bán kính đường tròn nội tiếp tam giác ABC là:

\(r = \dfrac{{\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}{p} = \sqrt {\dfrac{{\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{p}} \) ,

(với\(p = \dfrac{{10a.2 + 12a}}{2} = 16a\))\( = \sqrt {\dfrac{{\left( {16a - 10a} \right)\left( {16a - 10a} \right)\left( {16a - 12a} \right)}}{{16a}}}  = \sqrt {\dfrac{{6a.6a.4a}}{{16a}}}  = 3a\)

Ta có: \(\left\{ \begin{array}{l}SO \bot AB,\,\,\left( {do\,\,SO \bot \left( {ABC} \right)} \right)\\OI \bot AB\end{array} \right.\)

\( \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow \left( {\widehat {\left( {SAB} \right);\left( {ABC} \right)}} \right) = \widehat {SIO} = {45^0}\)

\( \Rightarrow \Delta SOI\) vuông cân tại O\( \Rightarrow SO = OI = r = 3a\)

Tính thể tích V của khối nón đã cho là: \(V = \dfrac{1}{3}\pi {r^2}.SO = \dfrac{1}{3}.\pi .{\left( {3a} \right)^2}.3a = 9\pi {a^3}\).

Chọn: A