Câu hỏi
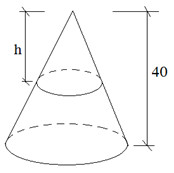
Một vật N1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N1 bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ N2 có thể tích bằng \(\dfrac{1}{8}\) thể tích N1.Tính chiều cao h của hình nón N2?
- A \(10cm\)
- B \(20cm\)
- C \(40cm\)
- D \(5cm\)
Phương pháp giải:
Công thức tính thể tích của khối nón có bán kính đáy và chiều cao \(h:\;\,V = \dfrac{1}{3}\pi {R^2}h.\)
Lời giải chi tiết:
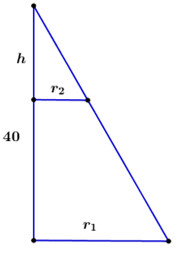
Gọi bán kính đáy của vật \({N_1}\) và vật \({N_2}\) lần lượt là \({r_1},\;{r_2}.\)
Khi đó ta có: \(\left\{ \begin{array}{l}{V_{{N_1}}} = \dfrac{1}{3}\pi r_1^2{h_1} = \dfrac{1}{3}\pi r_1^2.40 = \dfrac{{40\pi r_1^2}}{3}\\{V_{{N_2}}} = = \dfrac{1}{3}\pi r_2^2h = \dfrac{1}{3}\pi r_2^2h = \dfrac{{\pi r_2^2h}}{3}\end{array} \right.\)
Theo đề bài ta có:
\({V_{{N_1}}} = 8{V_{{N_2}}} \Leftrightarrow \dfrac{{40\pi r_1^2}}{3} = 8.\dfrac{{\pi r_2^2h}}{3} \Leftrightarrow 5r_1^2 = r_2^2h \Leftrightarrow \dfrac{{r_2^2}}{{r_1^2}} = \dfrac{5}{h}.\)
Do cắt vật \({N_1}\) bằng một mặt cắt song song với mặt đáy nên theo định lý Ta-lét ta có: \(\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{h}{{40}} \Rightarrow \dfrac{5}{h} = {\left( {\dfrac{h}{{40}}} \right)^2} \Leftrightarrow {h^3} = {5.40^2} = 8000 \Leftrightarrow h = 20cm.\)
Chọn B.







