Câu hỏi
Cho hình nón tròn xoay có độ dài đường sinh là \(2a\), góc ở đỉnh của hình nón bằng \(60^\circ \). Thể tích \(V\) của khối nón đã cho là
- A \(V = \dfrac{{\pi {a^3}}}{3}\).
- B \(V = \pi \sqrt 3 {a^3}\).
- C \(V = \pi {a^3}\).
- D \(V = \dfrac{{\pi \sqrt 3 {a^3}}}{3}\).
Phương pháp giải:
Thể tích khối nón là \(V=\dfrac{1}{3}\pi {{R}^{2}}h\) trong đó \(R;h\) lần lượt là bán kính đáy và chiều cao khối nón.
Lời giải chi tiết:
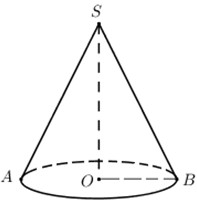
Ta có \(\widehat {ASB} = {60^0} \Rightarrow \widehat {OSB} = {30^0}\).
Xét tam giác vuông \(SOB\) ta có: \(\left\{ \begin{align} & OB=SB.\sin {{30}^{0}}=2a.\dfrac{1}{2}=a \\ & SO=SB.\cos {{30}^{0}}=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3} \\\end{align} \right.\)
\(\Rightarrow V=\dfrac{1}{3}\pi .O{{B}^{2}}.SO=\dfrac{1}{3}\pi {{a}^{2}}a\sqrt{3}=\dfrac{\pi {{a}^{3}}\sqrt{3}}{3}\).
Chọn D.
Câu hỏi trước
