Phương pháp giải:

Xác định hình chiếu H của S lên mặt phẳng (ABCD)

Thể tích của khối chóp S.ABCD là: \(V = \dfrac{1}{3}{S_{ABCD}}.SH\).

Lời giải chi tiết:

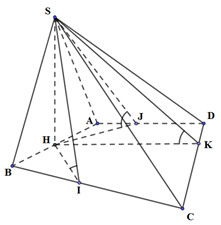
Gọi \(H\) là trung điểm của AB, do  tam giác SAB vuông cân tại S \( \Rightarrow SH \bot AB\) và \(SH = \dfrac{{AB}}{2} = \dfrac{a}{2}\)

Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right),\left( {SAB} \right) \cap \left( {ABCD} \right) = AB \Rightarrow SH \bot \left( {ABCD} \right)\)

Dựng \(HI \bot BC,HJ \bot AD,HK \bot CD\). Do góc tạo bởi các mặt phẳng \(\left( {SBC} \right),\)\(\left( {SCD} \right),\,\left( {SDA} \right)\) với mặt đáy lần lượt là \({60^0},\,{60^0},\,{60^0}\) nên \(\widehat {SIH} = \widehat {SJH} = \widehat {SKH} = {60^0}\)\( \Rightarrow \Delta SIH = \Delta SJH = \Delta SKH\,\left( {g.c.g} \right)\)\( \Rightarrow IH = JH = KH\)

\(\Delta SHI\) vuông tại H \( \Rightarrow HI = \dfrac{{SH}}{{\tan \widehat {SIH}}} = \dfrac{{\dfrac{a}{2}}}{{\tan {{60}^0}}} = \dfrac{a}{{2\sqrt 3 }}\)\( \Rightarrow IH = JH = KH = \dfrac{a}{{2\sqrt 3 }}\)

Ta có: \({S_{ABCD}} = {S_{HBC}} + {S_{HCD}} + {S_{HAC}} = \dfrac{1}{2}IH.BC + \dfrac{1}{2}JH.AD + \dfrac{1}{2}KH.CD = \dfrac{1}{2}.\dfrac{a}{{2\sqrt 3 }}.\left( {BC + AD + CD} \right)\)\( = \dfrac{1}{2}.\dfrac{a}{{2\sqrt 3 }}.\left( {9a - a} \right)\) (do chu vi tứ giác ABCD là 9a) \( = \dfrac{1}{2}.\dfrac{a}{{2\sqrt 3 }}.8a = \dfrac{{2{a^2}}}{{\sqrt 3 }}\)

Thể tích V của khối chóp S.ABCD là: \(V = \dfrac{1}{3}{S_{ABCD}}.SH = \dfrac{1}{3}.\dfrac{{2{a^2}}}{{\sqrt 3 }}.\dfrac{a}{2} = \)\(\dfrac{{{a^3}\sqrt 3 }}{9}\).

Chọn: D