Câu hỏi
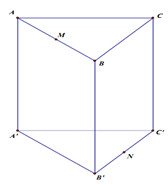
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh \(AB\) và \(B'C'\). Mặt phẳng \(\left( {A'MN} \right)\) cắt cạnh BC tại P. thể tích khối đa diện \(MBP.A'B'N\) là:
- A \(\dfrac{{\sqrt 3 {a^3}}}{{24}}\).
- B \(\dfrac{{7\sqrt 3 {a^3}}}{{96}}\).
- C \(\dfrac{{\sqrt 3 {a^3}}}{{12}}\).
- D \(\dfrac{{7\sqrt 3 {a^3}}}{{32}}\).
Phương pháp giải:
+) Thể tích hình chóp cụt: \(V = \dfrac{h}{3}\left( {B + B' + \sqrt {BB'} } \right)\) . Với \(B,B',h\)là diện tích hai đáy và chiều cao.
+) \(\left\{ \begin{array}{l}\left( P \right)//\left( Q \right)\\\left( \alpha \right) \cap \left( P \right) = a\\\left( \alpha \right) \cap \left( Q \right) = b\end{array} \right.\,\,\,\, \Rightarrow a//b\)
Lời giải chi tiết:
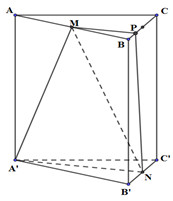
Ta có: \(\left\{ \begin{array}{l}\left( {ABC} \right)//\left( {A'B'C'} \right)\\\left( {A'MN} \right) \cap \left( {ABC} \right) = MP\\\left( {A'MN} \right) \cap \left( {A'B'C'} \right) = A'N\end{array} \right.\,\,\,\, \Rightarrow MP//A'N\)
Gọi \(E\) là trung điểm của \(BC\) ta có \(AE//A'N \Rightarrow MP//AE\). Lại có \(M\) là trung điểm của \(AB \Rightarrow P\) là trung điểm của \(BE\).
Dễ dàng chứng minh được: khối đa diện \(MBP.A'B'N\) là hình chóp cụt, có thể tích là:
\(V = \dfrac{{BB'}}{3}.\left( {{S_{BMP}} + {S_{A'B'N}} + \sqrt {{S_{BMP}}.{S_{A'B'N}}} } \right)\)
\({S_{BMP}} = \left( {\dfrac{{BM}}{{BA}}.\dfrac{{BP}}{{BC}}} \right).{S_{ABC}} = \dfrac{1}{2}.\dfrac{1}{4}.{S_{ABC}} = \dfrac{1}{8}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{{32}}\)
\({S_{A'B'N}} = \dfrac{{B'N}}{{B'C'}}.{S_{A'B'C'}} = \dfrac{1}{2}.{S_{A'B'C'}} = \dfrac{1}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{8}\)
\( \Rightarrow V = \dfrac{a}{3}.\left( {\dfrac{{{a^2}\sqrt 3 }}{8} + \dfrac{{{a^2}\sqrt 3 }}{{32}} + \sqrt {\dfrac{{{a^2}\sqrt 3 }}{8}.\dfrac{{{a^2}\sqrt 3 }}{{32}}} } \right) = \dfrac{a}{3}.\dfrac{{7{a^2}\sqrt 3 }}{{32}} = \dfrac{{7{a^3}\sqrt 3 }}{{96}}\).
Chọn: B







