Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\), SC tạo với đáy một giác \({60^0}\). Tính thể tích V của khối chóp đã cho.
- A \(V = \frac{{{a^3}\sqrt 6 }}{6}\).
- B \(V = \frac{{{a^3}\sqrt 3 }}{6}\).
- C \(V = \frac{{{a^3}\sqrt 6 }}{3}\).
- D \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\).
Phương pháp giải:
+) Xác định góc giữa đường thẳng \(SC\) và mặt đáy, góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
+) Sử dụng công thức tính thể tích \(V = \dfrac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
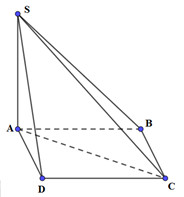
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {60^0}\)
\(ABCD\) là hình vuông cạnh a \( \Rightarrow AC = a\sqrt 2 ,\,\,\,{S_{ABCD}} = {a^2}\)
\(\Delta SAC\) vuông tại A \( \Rightarrow SA = AC.\tan \widehat {SCA} = a\sqrt 2 .\tan {60^0} = a\sqrt 2 .\sqrt 3 = a\sqrt 6 \)
Thể tích cần tìm là: \(V = \dfrac{1}{3}.SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 6 .{a^2} = \dfrac{{{a^3}\sqrt 6 }}{3}\).
Chọn: C







