Lời giải chi tiết:

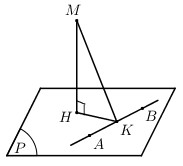
* Vẽ \(MH \bot \left( P \right),\,\,MK \bot AB\). Dễ thấy \(MK\) không đổi.

* Ta có \(MH \le MK\) \( \Rightarrow M{H_{\max }} = MK \Leftrightarrow H \equiv K\).

\( \Rightarrow \left( P \right)\) chứa \(AB\) và vuông góc với \(MK\).

* Giả sử \(K\left( {a;b;c} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MK}  = \left( {a - 1;b - 2;c - 3} \right)\\\overrightarrow {AB}  = \left( {2; - 1;1} \right)\end{array} \right.\)

\(\overrightarrow {MK} .\overrightarrow {AB}  = 0 \Rightarrow 2\left( {a - 1} \right) - 1\left( {b - 2} \right) + 1\left( {c - 3} \right) = 0 \Leftrightarrow 2a - b + c - 3 = 0\)  (1)

+) \(\left\{ \begin{array}{l}\overrightarrow {AK}  = \left( {a - 2;b + 2;c - 3} \right)\\\overrightarrow {AB}  = \left( {2; - 1;1} \right)\end{array} \right.;\,\,\overrightarrow {AK} //\overrightarrow {AB}  \Rightarrow \dfrac{{a - 2}}{2} = \dfrac{{b + 2}}{{ - 1}} = \dfrac{{c - 3}}{1} \Rightarrow \left\{ \begin{array}{l}a + 2b + 2 = 0\,\,\,\left( 2 \right)\\b + c - 1 = 0\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)

+) Giải hệ (1),(2),(3) \( \Rightarrow \left\{ \begin{array}{l}a = 0\\b =  - 1\\c = 2\end{array} \right. \Rightarrow K\left( {0; - 1;2} \right)\).

* \(\overrightarrow {{n_P}}  = \overrightarrow {MK}  = \left( { - 1; - 3; - 1} \right)//\left( {1;3;1} \right)\)

\( \Rightarrow Pt\left( P \right):\,\,1\left( {x - 0} \right) + 3\left( {y + 1} \right) + 1\left( {z - 2} \right) = 0 \Leftrightarrow x + 3y + z + 1 = 0\).

Chọn A.