Câu hỏi
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \(\left( {a \ne 0} \right)\) có đồ thị như hình dưới đây.
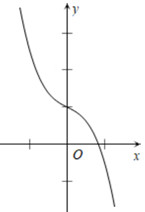
Khẳng định nào dưới đây đúng?
- A \(\left\{ \begin{array}{l}a < 0\\{b^2} - 3ac > 0\end{array} \right.\).
- B \(\left\{ \begin{array}{l}a < 0\\{b^2} - 3ac < 0\end{array} \right.\).
- C \(\left\{ \begin{array}{l}a > 0\\{b^2} - 3ac > 0\end{array} \right.\).
- D \(\left\{ \begin{array}{l}a > 0\\{b^2} - 3ac < 0\end{array} \right.\).
Phương pháp giải:
Dựa vào \(\underset{x\to +\infty }{\mathop{\lim }}\,y\Rightarrow \) Dấu của hệ số \(a\).
Dựa vào số điểm cực trị của đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0 \Rightarrow \) Loại các đáp án C và D.
Ta có \(y'=3a{{x}^{2}}+2bx+c\).
Do đồ thị hàm số không có cực trị \(\Rightarrow pt\,\,y'=0\) vô nghiệm.
\(\Delta '={{b}^{2}}-3ac<0\).
Vậy \(\left\{ \begin{align} & a<0 \\ & {{b}^{2}}-3ac<0 \\ \end{align} \right.\).
Chọn B.







