Lời giải chi tiết:

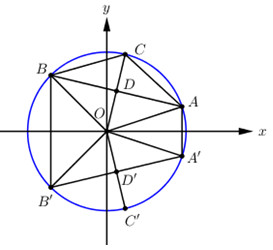
Do \({z_1},\,\,{z_2},\,\,{z_3}\) lần lượt được biểu diễn bởi các điểm \(A,\,\,B,\,\,C\). Gọi \(A',\,\,B',C'\) là các điểm đối xứng \(A,B,C\) qua \(Ox \Rightarrow \) \(A',\,\,B',C'\) lần lượt là các điểm biểu diễn số các số phức \(\overline {{z_1}} ,\,\,\overline {{z_2}} ,\,\,\overline {{z_3}} \) nên theo bài ra ta có: \(\left\{ \begin{array}{l}OA = OB = OC = OA' = OB' = OC' = 3\\\left| {\overrightarrow {OA'}  + \overrightarrow {OB'} } \right| = \left| {\overrightarrow {OC'} } \right| = 3\end{array} \right.\)

Gọi \(D'\) là trung điểm của \(A'B'\) ta có: \(\overrightarrow {OA'}  + \overrightarrow {OB'}  = 2\overrightarrow {OD'}  = \overrightarrow {OC'}  \Rightarrow D'\) là trung điểm của \(OC'\)\( \Rightarrow OD = \dfrac{3}{2}\).

Xét tam giác \(OA'B'\) ta có: \(O{D^2} = \dfrac{{OA{'^2} + OB{'^2}}}{2} - \dfrac{{A'B{'^2}}}{4}\)

\( \Leftrightarrow \dfrac{9}{4} = \dfrac{{9 + 9}}{2} - \dfrac{{A'B{'^2}}}{4} \Rightarrow A'B' = 3\sqrt 3  = AB\).

Áp dụng định lí Cosin trong tam giác \(OAB\) ta có:

\(\cos \angle AOB = \dfrac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}} = \dfrac{{9 + 9 - 27}}{{2.3.3}} = \dfrac{{ - 1}}{2} \Rightarrow \angle AOB = {120^0}\).

Gọi \(D\) là điểm đối xứng \(D'\) qua \(Ox\). Do \(D'\) là trung điểm của \(A'B'\) nên \(D\) là trung điểm của \(AB\).

\(D'\) là trung điểm của \(OC' \Rightarrow D\) là trung điểm của \(OC\).

Xét tứ giác \(OACB\) có hai đường chéo \(OC,\,\,AB\) cắt nhau tại trung điểm mỗi đường \( \Rightarrow OACB\) là hình bình hành \( \Rightarrow \angle ACB = \angle AOB = {120^0}\).

Chọn C.