Câu hỏi
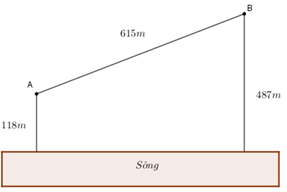
Cho hai vị trí A, B cách nhau \(615m\) , cùng nằm về một phía bờ song như hình vẽ. Khoảng cách từ A và từ B đến bờ song lần lượt là \(118m\) và \(487m\). Một người đi từ A đến bờ song lấy nước mang về B. Tính đoạn đường ngắn nhất mà người ấy có thể đi.
- A \(779,8m\)
- B \(671,4m\)
- C \(741,2m\)
- D \(596,5m\)
Phương pháp giải:
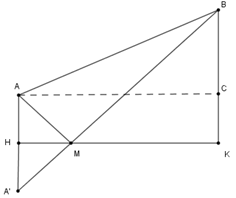
Lấy \(A'\) đối xứng với \(A\) qua bờ sông, nối \(A'B\) cắt bờ sông tại \(M\) khi đó ta có \(AM + MB = A'B\) là quãng đường ngắn nhất mà người đó đi.
Sử dụng định lý Pytago và định lý Ta-lét để tính toán.
Lời giải chi tiết:
Gọi \(H,K\) là hình chiếu của \(A,B\) trên bờ sông, lấy \(A'\) đối xứng với \(A\) qua bờ \(HK.\) Nối \(A'B\) cắt bờ \(HK\) tại \(M.\)
Suy ra \(AM = A'M.\)
Ta có \(AM + MB = A'M + MB \ge A'B\) nên quãng đường ngắn nhất người đó đi là \(AM + MB = \)\(A'B\).
Kẻ \(AC \bot BK\) tại \(C \Rightarrow AHKC\) là hình chữ nhật có
\(CK = AH = 118m \Rightarrow CB = BK - CK = 487 - 118 = 369m\)
Tam giác \(CAB\) vuông tại \(C \Rightarrow AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{615}^2} - {{369}^2}} = 492\) \( \Rightarrow HK = AC = 492m\)
Ta có \(HA'//BK \Rightarrow \frac{{HM}}{{MK}} = \frac{{A'M}}{{MB}} = \frac{{A'H}}{{BK}} = \frac{{118}}{{487}}\)
\(\begin{array}{l} \Rightarrow \frac{{HM}}{{MK}} = \frac{{118}}{{487}} \Rightarrow \frac{{HM}}{{HM + MK}} = \frac{{118}}{{118 + 487}} = \frac{{118}}{{605}} \Leftrightarrow \frac{{HM}}{{HK}} = \frac{{118}}{{605}}\\ \Leftrightarrow \frac{{HM}}{{492}} = \frac{{118}}{{605}} \Rightarrow HM = \frac{{58056}}{{605}}\end{array}\)
Xét tam giác \(HMA'\) có \(MA' = \sqrt {H{M^2} + H{{A'}^2}} = \sqrt {{{\left( {\frac{{58056}}{{605}}} \right)}^2} + {{118}^2}} \approx 152,093\)
Từ đó : \(\frac{{A'M}}{{MB}} = \frac{{118}}{{487}} \Rightarrow \frac{{A'M}}{{A'M + MB}} = \frac{{118}}{{118 + 487}} \Leftrightarrow \frac{{A'M}}{{A'B}} = \frac{{118}}{{605}} \Leftrightarrow A'B = \frac{{A'M.605}}{{118}} \approx 779,8m\)
Chọn A.