Câu hỏi
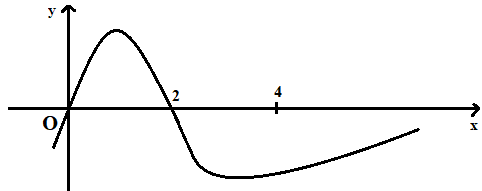
Giả sử hàm số \(y = f\left( x \right)\) có đạo hàm là hàm số \(y = f'\left( x \right)\) có đồ thị được cho như hình vẽ dưới đây và \(f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right)\). Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = f\left( x \right)\) trên \(\left[ {0;4} \right]\).
- A \(m = f\left( 4 \right)\)
- B \(m = f\left( 0 \right)\)
- C \(m = f\left( 2 \right)\)
- D \(m = f\left( 1 \right)\)
Phương pháp giải:
Lập bảng biến thiên của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\), từ đó tìm giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;4} \right]\).
Lời giải chi tiết:
Quan sát đồ thị hàm số \(y = f'\left( x \right)\) ta thấy:
+) Trên khoảng \(\left( {0;2} \right)\) thì \(f'\left( x \right) > 0\).
+) Trên khoảng \(\left( {2;4} \right)\) thì \(f'\left( x \right) < 0\).
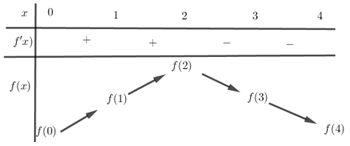
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy GTNN của hàm số đạt được bằng \(f\left( 0 \right)\) hoặc \(f\left( 4 \right)\).
Ta sẽ so sánh \(f\left( 0 \right)\) và \(f\left( 4 \right)\) như sau:
\(\begin{array}{l}f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right) \Leftrightarrow f\left( 0 \right) - f\left( 4 \right) = 2f\left( 2 \right) - f\left( 1 \right) - f\left( 3 \right)\\ = \left[ {f\left( 2 \right) - f\left( 1 \right)} \right] + \left[ {f\left( 2 \right) - f\left( 3 \right)} \right] > 0\,\,\,\left( {do\,\,f\left( 2 \right) > f\left( 1 \right),f\left( 2 \right) > f\left( 3 \right)} \right).\end{array}\)
Do đó \(f\left( 0 \right) - f\left( 4 \right) > 0 \Leftrightarrow f\left( 0 \right) > f\left( 4 \right)\).
Vậy \(m = f\left( 4 \right)\).
Chọn A.