Câu hỏi
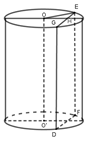
Cho hình trụ có bán kính đáy bằng \(a\sqrt 2 \). Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng \(\frac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích \(V\) của khối trụ đã cho.
- A \(V = \pi {a^3}\sqrt 3 \)
- B \(V = \frac{{2\pi {a^3}\sqrt 7 }}{3}\)
- C \(V = 2\pi {a^3}\sqrt 7 \)
- D \(V = \pi {a^3}\)
Phương pháp giải:
Tính chiều cao hình trụ và tính thể tích theo công thức \(V = \pi {R^2}h\).
Lời giải chi tiết:
Gọi \(O,O'\) lần lượt là tâm các đáy, khi đó thiết diện là hình vuông \(DGEF\) và \(d\left( {OO',\left( {DGEF} \right)} \right) = OH = \frac{a}{2}\).
Tam giác \(OEH\) vuông tại \(H\) nên \(HE = \sqrt {O{E^2} - O{H^2}} = \sqrt {2{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 7 }}{2}\)
\( \Rightarrow OO' = GD = GE = 2HE = a\sqrt 7 \).
Vậy thể tích \(V = \pi {R^2}h = \pi .{\left( {a\sqrt 2 } \right)^2}.a\sqrt 7 = 2\pi {a^3}\sqrt 7 \)
Chọn C.
Câu hỏi trước
