Phương pháp giải:

Dựng mặt phẳng chứa AB và song song trục d. Tính khoảng cách từ trục d đến mặt phẳng vừa dựng được.

Lời giải chi tiết:

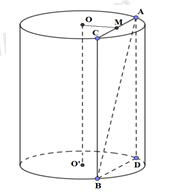
Gọi O, O’ lần lượt là tâm của hai hình tròn đáy (như hình vẽ). Dựng \(AD,\,\,BC\) song song OO’ , với  \(C \in \left( O \right)\), \(D \in \left( {O'} \right)\). Gọi M là trung điểm của AC.

Ta có: \(OO'//\left( {ACBD} \right) \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {ACBD} \right)} \right) = d\left( {O;\left( {ACBD} \right)} \right) = OM\),

(do \(OM \bot AC\), \(OM \bot AD\) \( \Rightarrow OM \bot \left( {ACBD} \right)\))

Ta có:  \(\left\{ \begin{array}{l}\widehat {\left( {AB;OO'} \right)} = {30^0}\\OO'//BC\end{array} \right. \Rightarrow \widehat {\left( {AB;BC} \right)} = \widehat {ABC} = {30^0}\)

\(\Delta ABC\) vuông tại C \( \Rightarrow AC = BC.\tan \widehat {ABC} = \sqrt 3 R.\dfrac{1}{{\sqrt 3 }} = R \Rightarrow MC = \dfrac{R}{2}\)

\(\Delta OMC\) vuông tại M \( \Rightarrow OM = \sqrt {O{C^2} - M{C^2}}  = \sqrt {{R^2} - \dfrac{{{R^2}}}{4}}  = \dfrac{{R\sqrt 3 }}{2}\)\( \Rightarrow d\left( {OO';AB} \right) = \dfrac{{R\sqrt 3 }}{2}\).

Chọn: A