Câu hỏi
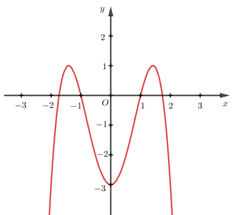
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
- A \(a < 0,b < 0,c < 0\)
- B \(a > 0,b < 0,c > 0\)
- C \(a < 0,b > 0,c < 0\)
- D \(a > 0,b < 0,c < 0\)
Phương pháp giải:
Quan sát, nhận xét dáng của đồ thị hàm số và suy ra điều kiện của \(a,\,\,b,\,\,c\,\).
Lời giải chi tiết:
Quan sát dáng đồ thị hàm số ta thấy \(a < 0\), loại B và D.
Đồ thị cắt trục \(Oy\) tại \(\left( {0; - 3} \right)\) nên \(c = - 3 < 0\).
Hàm số có ba điểm cực trị nên phương trình \(y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right) = 0\) có ba nghiệm phân biệt
\( \Leftrightarrow - \frac{b}{{2a}} > 0 \Leftrightarrow \frac{b}{{2a}} < 0 \Leftrightarrow b > 0\,\,\,\left( {do\,\,a < 0} \right).\)
Vậy \(a < 0,\,\,b > 0,\,\,c < 0\).
Chọn C.