Câu hỏi
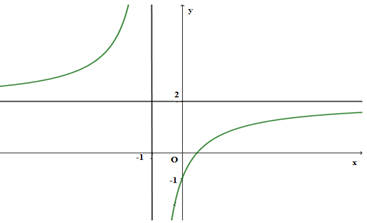
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
- A \(y = \frac{{1 - 2x}}{{x + 1}}\)
- B \(y = \frac{{2x - 1}}{{x + 1}}\)
- C \(y = \frac{{2x + 1}}{{x - 1}}\)
- D \(y = \frac{{2x + 1}}{{x + 1}}\)
Phương pháp giải:
Sử dụng: đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) nhận đường thẳng \(y = \frac{a}{c}\) làm đường tiệm cận ngang và dường thẳng \(x = - \frac{d}{c}\) làm đường tiệm cận đứng.
Tìm một số điểm mà đồ thị hàm số đi qua rồi thay tọa độ vào mỗi hàm số để loại trừ đáp án.
Lời giải chi tiết:
Từ hình vẽ ta thấy đồ thị nhận đường thẳng \(y = 2\) là đường tiệm cận ngang và đường thẳng \(x = - 1\) làm tiệm cận đứng. Và đồ thị hàm số đi qua điểm có tọa độ \(\left( {0; - 1} \right)\).
+ Đáp án A: Đồ thị \(y = \frac{{1 - 2x}}{{x + 1}}\) nhận \(y = - 2\) làm TCN và \(x = - 1\) làm TCĐ nên loại A.
+ Đáp án B: Đồ thị \(y = \frac{{2x + 1}}{{x + 1}}\) nhận \(y = 2\) làm TCN và \(x = - 1\) làm TCĐ và điểm có tọa độ \(\left( {0; - 1} \right)\) thuộc đồ thị nên chọn B.
+ Đáp án C: Đồ thị \(y = \frac{{2x + 1}}{{x - 1}}\) nhận \(y = 2\) làm TCN và \(x = 1\) làm TCĐ nên loại C.
+ Đáp án D: Đồ thị \(y = \frac{{2x + 1}}{{x + 1}}\) nhận \(y = 2\) làm TCN và \(x = - 1\) làm TCĐ nhưng điểm có tọa độ \(\left( {0; - 1} \right)\) không thuộc đồ thị nên loại D.
Chọn B.