Câu hỏi
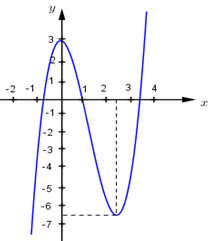
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt \(g\left( x \right) = f\left( {{x^2}} \right)\). Tìm số nghiệm của phương trình \(g'\left( x \right) = 0\).
- A 5
- B 4
- C
3
- D 2
Phương pháp giải:
+) Sử dụng công thức tính đạo hàm hàm hợp: \(y = f\left( {u\left( x \right)} \right)\,\, \Rightarrow \,\,y' = f'\left( {u\left( x \right)} \right).u'\left( x \right)\).
+) Tìm số nghiệm phân biệt của phương trình \(g'\left( x \right) = 0\).
Lời giải chi tiết:
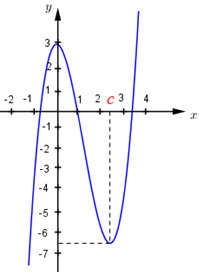
\(g\left( x \right) = f\left( {{x^2}} \right)\)\( \Rightarrow g'\left( x \right) = 2x.f'\left( x^2 \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow 2x.f'\left( {{x^2}} \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
f'\left( {{x^2}} \right) = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
\left[ \matrix{
{x^2} = 0 \hfill \cr
{x^2} = c \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = \pm \sqrt c \hfill \cr} \right.\)
(với \(2 < c < 3\), được biểu diễn trên hình vẽ bên)
Vậy, phương trình \(g'\left( x \right) = 0\) có 3 nghiệm.
Chọn: C







