Câu hỏi
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có \(f\left( 1 \right) = 1,\,\,f\left( { - 1} \right) = - \dfrac{1}{3}\). Đặt \(g\left( x \right) = {f^2}\left( x \right) - 4f\left( x \right)\). Cho biết đồ thị của \(y = f'\left( x \right)\) có dạng như hình vẽ dưới đây.
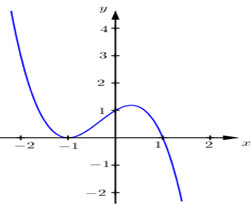
Mệnh đề nào sau đây đúng?
- A Hàm số \(g\left( x \right)\) có giá trị lớn nhất và không có giá trị nhỏ nhất trên \(\mathbb{R}\).
- B Hàm số \(g\left( x \right)\) có giá trị nhỏ nhất và không có giá trị lớn nhất trên \(\mathbb{R}\).
- C Hàm số \(g\left( x \right)\) có giá trị lớn nhất và giá trị nhỏ nhất trên \(\mathbb{R}\).
- D Hàm số \(g\left( x \right)\) không có giá trị lớn nhất và giá trị nhỏ nhất trên \(\mathbb{R}\).
Phương pháp giải:
+) Lập BBT của hàm số \(y = f\left( x \right)\) và nhận xét.
+) Lập BBT của hàm số \(y = g\left( x \right)\) và kết luận.
Lời giải chi tiết:
Bảng biến thiên của \(y = f\left( x \right)\):
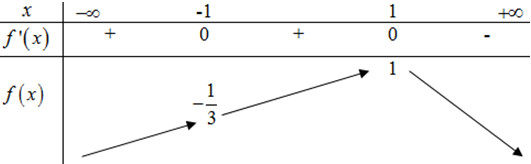
\( \Rightarrow f\left( x \right) \le 1,\forall x\)
Ta có: \(g\left( x \right) = {f^2}\left( x \right) - 4f\left( x \right) \Rightarrow g'\left( x \right) = 2f\left( x \right).f'\left( x \right) - 4f'\left( x \right) = 2f'\left( x \right).\left( {f\left( x \right) - 2} \right)\)
Mà \(f\left( x \right) - 2 < 0,\,\,\forall x\) (do \(f\left( x \right) \le 1,\forall x\))
Ta có bảng biến thiên của \(y = g\left( x \right)\) như sau:
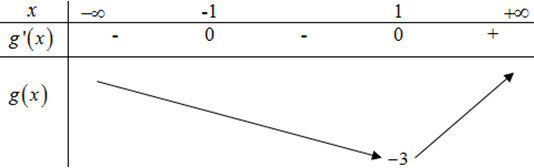
Chọn: B







