Câu hỏi
Cho hình lăng trụ \(ABC.\,A'B'C'\) có thể tích bằng \(V\). Gọi \(M\) là trung điểm cạnh \(BB'\), điểm \(N\) thuộc cạnh \(CC'\) sao cho \(CN = 2C'N\). Tính thể tích khối chóp \(A.\,BCNM\) theo \(V\).
- A \({V_{A.BCNM}} = \dfrac{{7V}}{{12}}\).
- B \({V_{A.BCNM}} = \dfrac{{7V}}{{18}}\).
- C \({V_{A.BCNM}} = \dfrac{V}{3}\).
- D \({V_{A.BCNM}} = \dfrac{{5V}}{{18}}\).
Phương pháp giải:
+) So sánh diện tích hình thang \(BMNC\) và diện tích hình bình hành \(BCC'B'\) từ đó suy ra tỉ số thể tích \(\dfrac{{{V_{A.BMNC}}}}{{{V_{A.BCC'B'}}}}\).
+) So sánh \({V_{A.BCC'B'}}\) với \(V\).
Lời giải chi tiết:
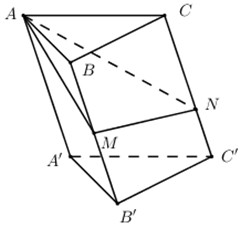
Ta có
\(\begin{array}{l}{S_{BCC'B'}} = d\left( {B;CC'} \right).CC'\\{S_{BMNC}} = \dfrac{{\left( {BM + CN} \right)d\left( {B;CC'} \right)}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}d\left( {B;CC'} \right)\left( {\dfrac{1}{2}CC' + \dfrac{2}{3}CC'} \right) = \dfrac{7}{{12}}d\left( {B;CC'} \right).CC'\end{array}\)
\( \Rightarrow \dfrac{{{S_{BMNC}}}}{{{S_{BCC'B'}}}} = \dfrac{7}{{12}} \Rightarrow \dfrac{{{V_{A.BMNC}}}}{{{V_{A.BCC'B'}}}} = \dfrac{7}{{12}} \Rightarrow {V_{A.BMNC}} = \dfrac{7}{{12}}{V_{A.BCC'B'}}\).
Mà \({V_{A.BCC'B'}} = \dfrac{2}{3}V \Rightarrow {V_{A.BMNC}} = \dfrac{7}{{12}}.\dfrac{2}{3}V = \dfrac{7}{{18}}V\).
Chọn B.







