Câu hỏi
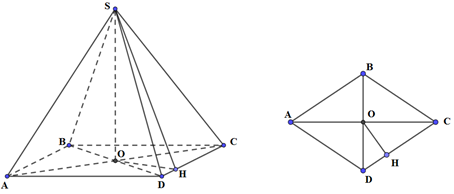
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, \(\angle BAD = 60^\circ \), \(SO \bot \left( {ABCD} \right)\) và mặt phẳng (SCD) tạo với đáy một góc \(60^\circ \). Tính thế tích khối chóp S.ABCD.
- A \(\frac{{\sqrt 3 {a^3}}}{{12}}\).
- B \(\frac{{\sqrt 3 {a^3}}}{8}\).
- C \(\frac{{\sqrt 3 {a^3}}}{{48}}\).
- D \(\frac{{\sqrt 3 {a^3}}}{{24}}\).
Phương pháp giải:
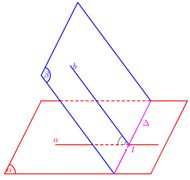
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right).\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right):\;\angle \left( {\left( \alpha \right);\left( \beta \right)} \right) = \angle \left( {a;\;b} \right).\)
Lời giải chi tiết:
Kẻ \(OH \bot CD,\left( {H \in CD} \right)\). Ta có: \(\left\{ \begin{array}{l}CD \bot OH\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOH} \right)\,\, \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle SHO = {60^0}\)
ABCD là hình thoi tâm O, \(\angle BAD = 60^\circ \Rightarrow \Delta BCD\) đều, \(OH = \frac{1}{2}d\left( {B;CD} \right) = \frac{1}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4}\)
\(\Delta SOH\) vuông tại O \( \Rightarrow SO = OH.\tan \angle H = \frac{{a\sqrt 3 }}{4}.\tan {60^0} = \frac{{3a}}{4}\)
Diện tích hình thoi ABCD: \({S_{ABCD}} = 2{S_{ABC}} = 2.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\)
Tính thế tích khối chóp S.ABCD: \({V_{S.ABCD}} = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.\frac{{3a}}{4}.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{8}\).
Chọn: B