Câu hỏi
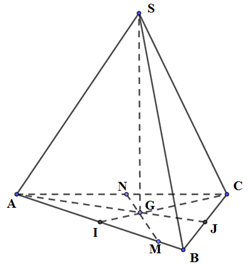
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất \({V_{\min }}\) của khối tứ diện SAMN.
- A \({V_{\min }} = \frac{{\sqrt 2 }}{{27}}\).
- B \({V_{\min }} = \frac{4}{9}\).
- C \({V_{\min }} = \frac{{\sqrt 2 }}{{18}}\).
- D \({V_{\min }} = \frac{{\sqrt 2 }}{{36}}\).
Phương pháp giải:
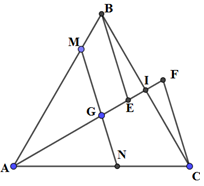
Cho tam giác đều ABC, G là trọng tâm tam giác ABC. Đường thẳng qua G cắt AB, AC lần lượt tại M, N. Khi đó, \(\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = 3\)
Thật vậy, gọi I là trung điểm của BC, qua B, C kẻ các đường thẳng song song MN, cắt đường thẳng AI tại E, F.
Khi đó, \(\Delta BIE = \Delta CIF \Rightarrow IE = IF\)
Ta có: \(\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = \frac{{AE}}{{AG}} + \frac{{AF}}{{AG}} = \frac{{AE + AF}}{{AG}} = \frac{{2.AI}}{{AG}} = \frac{{2.AI}}{{\frac{2}{3}AI}} = 3\;\;\;\left( {do\;\;IE = IF} \right)\)
Lời giải chi tiết:
Do SABC là tứ diện đều, G là trọng tâm tam giác ABC
\( \Rightarrow SG \bot \left( {ABC} \right)\)
\( \Rightarrow \)Thể tích khối tứ diện SAMN: \(V = \frac{1}{3}.SG.{S_{AMN}}\)
+) Tam giác ABC đều, cạnh bằng 1 \( \Rightarrow AJ = \frac{{1.\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2} \Rightarrow AG = \frac{2}{3}.AJ = \frac{{\sqrt 3 }}{3}\)
Tam giác SAG vuông tại G \( \Rightarrow SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {1 - \frac{1}{3}} = \sqrt {\frac{2}{3}} \)
+) Diện tích tam giác AMN: \({S_{AMN}} = \frac{1}{2}.AN.AM.\sin A = \frac{1}{2}.AN.AM.\sin 60^\circ = \frac{{\sqrt 3 }}{4}.AN.AM\)
Ta có: \(\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = 3 \Leftrightarrow \frac{1}{{AM}} + \frac{1}{{AN}} = 3\)
Mà \(\frac{1}{{AM}} + \frac{1}{{AN}} \ge \frac{2}{{\sqrt {AM.AN} }} \Rightarrow 3 \ge \frac{2}{{\sqrt {AM.AN} }} \Rightarrow \frac{{\sqrt {AM.AN} }}{2} \ge \frac{1}{3} \Rightarrow AM.AN \ge \frac{4}{9}\)
\(\begin{array}{l} \Rightarrow {S_{AMN}} = \frac{{\sqrt 3 }}{4}.AN.AM \ge \frac{{\sqrt 3 }}{4}.\frac{4}{9} = \frac{{\sqrt 3 }}{9}\\ \Rightarrow {V_{SAMN}} \ge \frac{1}{3}.\sqrt {\frac{2}{3}} .\frac{{\sqrt 3 }}{9} = \frac{{\sqrt 2 }}{{27}}\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(AM = AN = \frac{2}{3}\)
\( \Rightarrow \left( {{V_{SAMN}}} \right)\min = \frac{{\sqrt 2 }}{{27}}\) khi và chỉ khi \(AM = AN = \frac{2}{3}\) hay MN là đường thẳng qua G song song với BC
Chọn: A