Câu hỏi
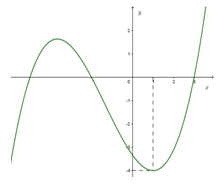
Cho hàm số \(f\left( x \right)\) có đồ thị như hình vẽ bên. Bất phương trình \(f\left( {{e^x}} \right) < m\left( {3{e^x} + 2019} \right)\) có nghiệm \(x \in \left( {0;1} \right)\) khi và chỉ khi
- A \(m > - \dfrac{4}{{1011}}\)
- B \(m \ge - \dfrac{4}{{3e + 2019}}\)
- C \(m > - \dfrac{2}{{1011}}\)
- D \(m > \dfrac{{f\left( e \right)}}{{3e + 2019}}\)
Phương pháp giải:
Đặt \({e^x} = t\left( {t > 0} \right)\). Ta đưa bất phương trình đã cho thánh bất phương trình ẩn \(t\), từ đó lập luận để có phương trình ẩn \(t\) có nghiệm thuộc \(\left( {1;e} \right).\)
Ta chú ý rằng hàm số \(y = f\left( x \right)\) và \(y = f\left( t \right)\) có tính chất giống nhau nên từ đồ thị hàm số đã cho ta suy ra tính chất hàm \(f\left( t \right).\)
Sử dụng phương pháp hàm số để tìm \(m\) sao cho bất phương trình có nghiệm.
Bất phương trình \(m > f\left( X \right)\) có nghiệm trân \(\left( {a;b} \right)\) khi \(m > \mathop {\min }\limits_{\left[ {a;b} \right]} \,f\left( X \right)\)
Lời giải chi tiết:
Xét bất phương trình \(f\left( {{e^x}} \right) < m\left( {3{e^x} + 2019} \right)\) (*)
Đặt \({e^x} = t\left( {t > 0} \right)\). Với \(x \in \left( {0;1} \right) \Rightarrow t \in \left( {{e^0};{e^1}} \right) \Rightarrow t \in \left( {1;e} \right)\)
Ta được bất phương trình \(f\left( t \right) < m\left( {3t + 2019} \right) \Leftrightarrow m > \dfrac{{f\left( t \right)}}{{3t + 2019}}\) (1) (vì \(3t + 2019 > 0\) với \(t \in \left( {1;e} \right)\))
Để bất phương trình (*) có nghiệm \(x \in \left( {0;1} \right)\) thì bất phương trình (1) có nghiệm \(t \in \left( {1;e} \right)\).
Ta xét hàm \(g\left( t \right) = \dfrac{{f\left( t \right)}}{{3t + 2019}}\) trên \(\left( {1;e} \right)\)
Ta có \(g'\left( t \right) = \dfrac{{f'\left( t \right)\left( {3t + 2019} \right) - 3f\left( t \right)}}{{{{\left( {3t + 2019} \right)}^2}}}\)
Nhận xét rằng đồ thị hàm số \(y = f\left( t \right)\)có tính chất giống với đồ thị hàm số \(y = f\left( x \right)\) nên xét trên khoảng \(\left( {1;e} \right)\) ta thấy rằng \(f\left( t \right) < 0\) và đồ thị hàm số đi lên từ trái qua phải hay hàm số đồng biến trên \(\left( {1;e} \right)\) nên \(f'\left( t \right) > 0\).
Từ đó \(g'\left( t \right) = \dfrac{{f'\left( t \right)\left( {3t + 2019} \right) - 3f\left( t \right)}}{{{{\left( {3t + 2019} \right)}^2}}} > 0\) với \(t \in \left( {1;e} \right)\) hay hàm số \(g\left( t \right)\) đồng biến trên \(\left( {1;e} \right)\)
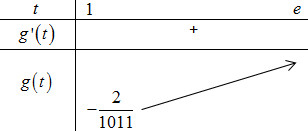
Từ BBT ta thấy để bất phương trình \(m > \dfrac{{f\left( t \right)}}{{3t + 2019}}\) có nghiệm \(t \in \left( {1;e} \right)\) thì \(m > \mathop {\min }\limits_{\left[ {1;e} \right]} g\left( t \right) \Leftrightarrow m > - \dfrac{2}{{1011}}.\)
Chọn C.







