Câu hỏi
Hình chóp tam giác đều \(S.ABC\) có cạnh đáy là \(a\) và mặt bên tạo với đáy góc \({45^0}\). Tính theo \(a\) thể tích khối chóp \(S.ABC\).
- A \(\dfrac{{{a^3}}}{8}\)
- B \(\dfrac{{{a^3}}}{{24}}\)
- C \(\dfrac{{{a^3}}}{{12}}\)
- D \(\dfrac{{{a^3}}}{4}\)
Phương pháp giải:
Tính diện tích đáy và chiều cao rồi áp dụng công thức \(V = \dfrac{1}{3}Sh\) tính thể tích.
Lời giải chi tiết:
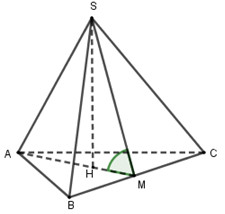
Gọi \(H\) là tâm đường tròn ngoại tiếp tam giác đều \(ABC\) suy ra \(SH\) là đường cao.
Góc giữa mặt bên và đáy là góc giữa \(SM\) và \(AM\) vơí \(M\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều cạnh \(a\) nên \(AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow MH = \dfrac{1}{3}AM = \dfrac{{a\sqrt 3 }}{6}\)
Tam giác vuông \(SHM\) có \(MH = \dfrac{{a\sqrt 3 }}{6},\,\,\widehat {SMH} = {45^0}\) nên \(SH = HM = \dfrac{{a\sqrt 3 }}{6}\).
Vậy thể tích \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 3 }}{6} = \dfrac{{{a^3}}}{{24}}\).
Chọn B.
Câu hỏi trước
