Phương pháp giải:

- Chia khối đa diện \(ABCSFH\) thành hai khối chóp \(A.BCHF\) và \(S.BCHF\) rồi tính thể tích.

Lời giải chi tiết:

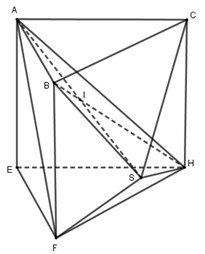
Gọi \(I\) là hình chiếu của \(A\) lên \(BH\). Khi đó \(S\) đối xứng với \(A\) qua \(BH\) hay \(S\) đối xứng với \(A\) qua \(I\).

Chia khối đa diện \(ABCSFH\) thành hai khối chóp \(A.BCHF\) và \(S.BCHF\) thì ta có \({V_{ABCHFS}} = {V_{A.BCHF}} + {V_{S.BCHF}}\)

Lại có \(SI = AI\) và \(SA \cap \left( {BCHF} \right)\) tại \(I\) nên

\(d\left( {A,\left( {BCHF} \right)} \right) = d\left( {S,\left( {BCHF} \right)} \right)\).

Suy ra \({V_{A.BCHF}} = {V_{S.BCHF}} \Rightarrow {V_{ABCHFS}} = 2{V_{A.BCHF}}\)

Dễ thấy \({V_{A.BCHF}} = {V_{ABC.EFH}} - {V_{A.EFH}} = {V_{ABC.EFH}} - \dfrac{1}{3}{V_{ABC.EFH}} = \dfrac{2}{3}{V_{ABC.EFH}}\)

Mà \({V_{ABC.EFH}} = AE.{S_{ABC}} = a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{4}\) nên \({V_{A.BCHF}} = \dfrac{2}{3}{V_{ABC.EFH}} = \dfrac{2}{3}.\dfrac{{{a^3}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{6}\)

\( \Rightarrow {V_{ABCHFS}} = 2{V_{A.BCHF}} = 2.\dfrac{{{a^3}\sqrt 3 }}{6} = \dfrac{{{a^3}\sqrt 3 }}{3}\).

Vậy \({V_{ABCHFS}} = \dfrac{{{a^3}\sqrt 3 }}{3}\).

Chọn D.