Câu hỏi
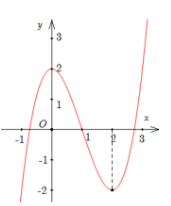
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\cos x} \right) = m\) có 2 nghiệm phân biệt thuộc \(\left( {0;\dfrac{{3\pi }}{2}} \right]\) là:
- A \(\left[ { - 2;2} \right]\)
- B \(\left( {0;2} \right)\)
- C \(\left( { - 2;2} \right)\)
- D \(\left[ {0;2} \right)\)
Phương pháp giải:
+) Đặt \(t = \cos x\), xác định khoảng giá trị của \(t\), khi đó phương trình trở thành \(f\left( t \right) = m\).
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và \(y = m\) song song với trục hoành.
Lời giải chi tiết:
Đặt \(t = \cos x\) ta có \(x \in \left( {0;\dfrac{{3\pi }}{2}} \right] \Rightarrow t \in \left[ { - 1;1} \right)\), khi đó phương trình trở thành \(f\left( t \right) = m\).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và \(y = m\) song song với trục hoành.
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta thấy phương trình \(f\left( t \right) = m\) có 2 nghiệm phân biệt thuộc \(\left[ { - 1;1} \right)\) khi và chỉ khi \(m \in \left( {0;2} \right)\).
Chọn B.