Câu hỏi
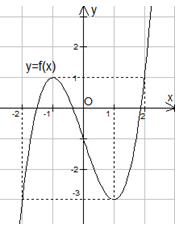
Cho hàm số \(y = f(x)\) liên tục trên R và có đồ thị như hình bên. Phương trình \(f(2\sin x) = m\) có đúng ba nghiệm phân biệt thuộc đoạn \(\left[ { - \pi ;\pi } \right]\)khi và chỉ khi
- A \(m \in \left\{ { - 3;1} \right\}\)
- B \(m \in \left( { - 3;1} \right)\)
- C \(m \in \left[ { - 3;1} \right)\)
- D \(m \in \left( { - 3;1} \right]\)
Phương pháp giải:
+) Đặt \(t = 2\sin x\), xác định điều kiện của \(t.\)
+) Khi đó phương trình trở thành \(f\left( t \right) = m\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = m\) song song với trục hoành.
Lời giải chi tiết:
Đặt \(t = 2\sin x\), với \(x \in \left[ { - \pi ;\pi } \right] \Rightarrow t \in \left[ { - 2;2} \right]\).
Khi đó phương trình trở thành \(f\left( t \right) = m\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = m\) song song với trục hoành.
Với mỗi \(t \in \left( { - 2;2} \right)\) sẽ cho ta 2 nghiệm \(x \in \left[ { - \pi ;\pi } \right]\), khi \(t = \pm 2\) cho ta 1 nghiệm \(x\).
Khi đó phương trình ban đầu có 3 nghiệm \(x \in \left[ { - \pi ;\pi } \right] \Rightarrow \)Phương trình \(f\left( t \right) = m\) có 1 nghiệm \(t = 2\) và một nghiệm \(t \in \left( { - 2;2} \right)\) hoặc phương trình \(f\left( t \right) = m\) có 1 nghiệm \(t = - 2\) và một nghiệm \(t \in \left( { - 2;2} \right)\).
\( \Rightarrow m = 1\) hoặc \(m = - 3 \Rightarrow m \in \left\{ {1; - 3} \right\}\).
Chọn A.