Môn Toán - Lớp 12
30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ nhận biết
Câu hỏi
Cho hàm số \(y = f\left( x \right)\) và có bảng biến thiên trên \({\rm{[}} - 5;7)\) như sau:
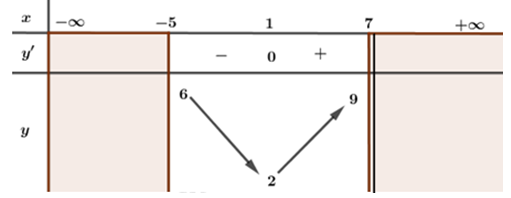
Mệnh đề nào sau đây đúng?
- A \(\mathop {\min f\left( x \right)}\limits_{[ - 5;7)} = 2\) và hàm số không đạt giá trị lớn nhất trên \({\rm{[}} - 5;7)\)
- B \(\mathop {\max }\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 6\) và \(\mathop {min}\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 2\)
- C \(\mathop {\max }\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 9\) và \(\mathop {min}\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 2\)
- D \(\mathop {\max }\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 9\) và \(\mathop {min}\limits_{{\rm{[}} - 5;7)} f\left( x \right) = 6\)
Phương pháp giải:
Dựa vào BBT để nhận xét các GTLN và GTNN của hàm số trên khoảng cần xét.
Lời giải chi tiết:
Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left[ { - 5;\;7} \right)} f\left( x \right) = 2\;\;khi\;\;x = 1\) và hàm số không tồn tại GTLN trên \(\left[ { - 5;\;7} \right).\)
Chọn A.
Câu hỏi trước
