Câu hỏi
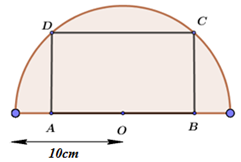
Tính diện tích lớn nhất của hình chữ nhật \(ABCD\) nội tiếp trong nửa đường tròn có bán kính \(10cm\) (hình vẽ)
- A \(160c{m^2}\)
- B \(100c{m^2}\)
- C \(80c{m^2}\)
- D \(200c{m^2}\)
Phương pháp giải:
+) Đặt \(OA = x\) \(\left( {x > 0} \right)\). Tính \(AB\) và \(AD\) theo \(x\).
+) Áp dụng BĐT Cô-si cho hai số không âm \(a,\,\,b:\,\,ab \le \frac{{{a^2} + {b^2}}}{2}\). Dấu “=” xảy ra \( \Leftrightarrow a = b\).
Lời giải chi tiết:
Đặt \(OA = x \Rightarrow AB = 2x\) \(\left( {x > 0} \right)\).
Áp dụng định lí Pytago trong tam giác vuông \(OAD\) ta có:
\(AD = \sqrt {O{D^2} - O{A^2}} = \sqrt {100 - {x^2}} \)
\( \Rightarrow {S_{ABCD}} = AB.AD = 2x.\sqrt {100 - {x^2}} \le {x^2} + 100 - {x^2} = 100\)
Vậy diện tích lớn nhất của hình chữ nhật \(ABCD\) là \(100c{m^2}\), dấu “=” xảy ra \( \Leftrightarrow {x^2} = 100 - {x^2} \Leftrightarrow x = 5\sqrt 2 \,\,\left( {cm} \right)\).
Chọn B.