Phương pháp giải:

Hàm số \(y = f\left( x \right)\)  nghịch biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \le 0\;\;\forall x \in \left( {a;\;b} \right)\) và bằng 0 tại hữu hạn điểm.

Lời giải chi tiết:

Ta có: \(y' =  - {x^2} + 2x - m\)

Hàm số đã cho nghịch biến trên \(\left( {0; + \infty } \right) \Leftrightarrow y' \le 0\;\;\forall x \in \left( {0; + \infty } \right).\)

\( \Leftrightarrow  - {x^2} + 2x - m \le 0\;\;\forall x \in \left( {0; + \infty } \right) \Leftrightarrow {x^2} - 2x \ge  - m\;\;\forall x \in \left( {0; + \infty } \right)\;\;\;\left( * \right)\)

Xét hàm số \(g\left( x \right) = {x^2} - 2x\)\( \Rightarrow \left( * \right) \Leftrightarrow  - m \le \mathop {Min}\limits_{\left( {0; + \infty } \right)} g\left( x \right).\)

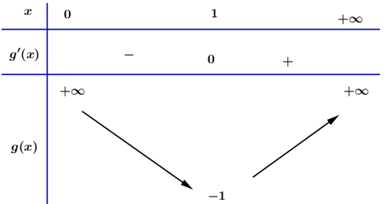
Ta có: \(g'\left( x \right) = 2x - 2 = 0 \Leftrightarrow x = 1.\) Khi đó ta có BBT:

\( \Rightarrow  - m \le \mathop {Min}\limits_{\left( {0; + \infty } \right)} g\left( x \right) \Leftrightarrow  - m \le  - 1 \Leftrightarrow m \ge 1.\)

Chọn A.