Câu hỏi
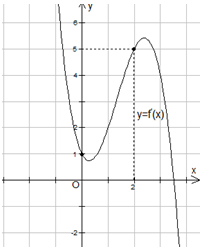
Cho hàm số \(y = f(x)\) có đồ thị đạo hàm \(y = f'(x)\) như hình bên.
Khẳng định nào sau đây là đúng?
- A Hàm số \(y = f(x) - {x^2} - x\) đạt cực đại tại \(x = 0\)
- B Hàm số \(y = f(x) - {x^2} - x\) đạt cực tiểu tại \(x = 0\)
- C Hàm số \(y = f(x) - {x^2} - x\) không đạt cực trị tại \(x = 0\)
- D Hàm số \(y = f(x) - {x^2} - x\) không có cực trị.
Phương pháp giải:
+) Quan sát đồ thị hàm số đã cho, và các đáp án trong đề bài, chọn ra câu đúng.
+) \(x = {x_0}\) là điểm cực trị của hàm số \(y = f\left( x \right) \Rightarrow f'\left( {{x_0}} \right) = 0.\)
+) Số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\) là số nghiệm bội lẻ của phương trình \(f'\left( x \right) = 0.\)
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) - {x^2} - x \Rightarrow y' = f'\left( x \right) - 2x - 1.\)
\( \Rightarrow y' = 0 \Leftrightarrow f'\left( x \right) - 2x - 1 = 0 \Leftrightarrow f'\left( x \right) = 2x + 1\)
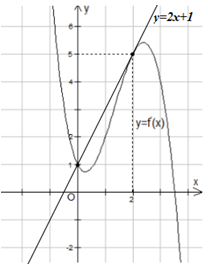
Số nghiệm của phương trình \(f'\left( x \right) = 2x + 1\) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và \(y = 2x + 1\).
Dựa vào đồ thị hàm số ta thấy phương trình \(f'\left( x \right) = 2x + 1\) có 2 nghiệm \(x = 0\) và \(x = 2\), tuy nhiên chỉ qua nghiệm \(x = 0\) thì \(y'\) đổi dấu, do đó hàm số có 1 cực trị \(x = 0\).
Mà qua điểm \(x=0\) thì y' đổi dấu từ dương sang âm nên \(x=0\) là điểm cực đại của hàm số.
Chọn A.