Câu hỏi
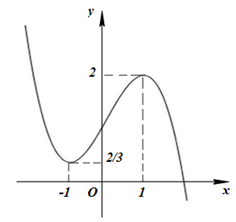
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới :
Số giá trị nguyên dương của \(m\) để phương trình \(f\left( {{x^2} - 4x + 5} \right) + 1 = m\) có nghiệm là
- A \(0\)
- B Vô số
- C \(4\)
- D \(3\)
Phương pháp giải:
+) Đặt \(t = {x^2} - 4x + 5\), xác định điều kiện của t.
+) Đưa phương trình về dạng \(f\left( t \right) = m - 1\), dựa vào đồ thị hàm số tìm điều kiện của m để phương trình có nghiệm t thỏa mãn điều kiện của chính nó.
Lời giải chi tiết:
Đặt \(t = {x^2} - 4x + 5 = {\left( {x - 2} \right)^2} + 1 \ge 1\), phương trình trở thành \(f\left( t \right) = m - 1\).
Số nghiệm của phương trình \(f\left( t \right) = m - 1\) là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thăngr \(y = m - 1\).
Dựa vào đồ thị hàm số ta thấy phương trình \(f\left( t \right) = m - 1\) có nghiệm \(t \ge 1 \Leftrightarrow m - 1 \le 2 \Leftrightarrow m \le 3\).
Kết hợp điều kiện m nguyên dương \( \Rightarrow m \in \left\{ {1;2;3} \right\}\).
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn D.