Câu hỏi
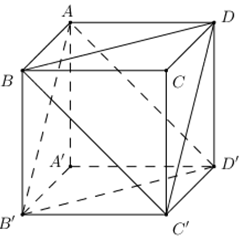
Cho khối lập phương \(ABCD.A'B'C'D'.\) Cắt khối lập phương trên bởi các mặt phẳng \(\left( {AB'D'} \right)\) và \(\left( {C'BD} \right)\) ta được ba khối đa diện. Xét các mệnh đề sau :
(I) : Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II) : Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III) : Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là :
- A \(2\)
- B \(1\)
- C \(3\)
- D \(0\)
Phương pháp giải:
Chia khối lập phương, nhận xét các khối tạo thành và tính thể tích của chúng.
Lời giải chi tiết:
Chia khối lập phương \(ABC.A'B'C'\) bởi mặt phẳng \(\left( {AB'D'} \right)\) và \(\left( {C'BD} \right)\) ta được :
+) Chóp \(A.A'B'D'\).
+) Chóp \(C'.BCD\)
+) Khối bát diện \(ABD.B'C'D'\).
Ta có \({V_{A.A'B'D'}} = \frac{1}{3}AA'.{S_{A'B'D'}} = \frac{1}{3}AA'.\frac{1}{2}A'B'.A'D' = \frac{1}{6}{V_{ABCD.A'B'C'D'}}\)
Tương tự ta có \({V_{C'.BCD}} = \frac{1}{6}{V_{ABCD.A'B'C'D'}}\).
\( \Rightarrow {V_{ABD.B'C'D'}} = \frac{2}{3}{V_{ABD.B'C'D'}}\).
Các khối \(A.A'B'D'\) và \(C'.BCD\) không phải là chóp tam giác đều và khối bát diện \(ABD.B'C'D'\) không phải khối bát diện đều.
Do đó chỉ có mệnh đề III đúng.
Chọn B.