Câu hỏi
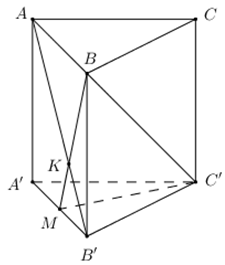
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\) và \(AB' \bot BC'\) . Tính thể tích \(V\) của khối lăng trụ đã cho.
- A \(V = \frac{{{a^2}\sqrt 6 }}{4}\)
- B \(V = \frac{{7{a^3}}}{8}\)
- C \(V = {a^3}\sqrt 6 \)
- D \(V = \frac{{{a^3}\sqrt 6 }}{8}\)
Phương pháp giải:
+) Chứng minh \(AB' \bot BM\) với M là trung điểm của A’B’.
+) Gọi \(K = AB' \cap CM\). Gọi \(AA' = h\). Tính B’K, BM theo \(a,\,\,h\).
+) Sử dụng hệ thức lượng trong tam giác vuông BB’M tính h theo a.
+) Tính thể tích lăng trụ \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}}\).
Lời giải chi tiết:
Gọi M là trung điểm của \(A'B'\) ta có
\(\left\{ \begin{array}{l}C'M \bot A'B'\\C'M \bot AA'\end{array} \right. \Rightarrow C'M \bot \left( {ABB'A'} \right) \Rightarrow C'M \bot AB'\)
\(\left\{ \begin{array}{l}BC' \bot AB'\\C'M \bot AB'\end{array} \right. \Rightarrow AB' \bot \left( {BC'M} \right) \Rightarrow AB' \bot BM\).
Gọi \(K = AB' \cap CM\).
Áp dụng định lí Ta-lét ta có :
\(\frac{{B'K}}{{AK}} = \frac{{MB'}}{{AB}} = \frac{1}{2} \Rightarrow B'K = \frac{1}{2}AK \Rightarrow B'K = \frac{{AB'}}{3}\)
Đặt \(AA' = BB' = CC' = DD' = h\).
Ta có : \(BM = \sqrt {{h^2} + \frac{{{a^4}}}{4}} ;\,\,AB' = \sqrt {{a^2} + {h^2}} \Rightarrow B'K = \frac{{\sqrt {{a^2} + {h^2}} }}{3}\)
Áp dụng hệ thức lượng trong tam giác vuông BB’M ta có :
\(\begin{array}{l}B'K.BM = BB'.B'M \Leftrightarrow \frac{1}{3}\sqrt {{a^2} + {h^2}} .\sqrt {{h^2} + \frac{{{a^2}}}{4}} = h.\frac{a}{2}\\ \Leftrightarrow 2\sqrt {{a^2} + {h^2}} .\sqrt {{h^2} + \frac{{{a^2}}}{4}} = 3ah \Leftrightarrow \left( {{a^2} + {h^2}} \right)\left( {4{h^2} + {a^2}} \right) = 9{a^2}{h^2}\\ \Leftrightarrow 4{a^2}{h^2} + {a^4} + 4{h^4} + {a^2}{h^2} = 9{a^2}{h^2} \Leftrightarrow {a^4} - 4{a^2}{h^2} + 4{h^4} = 0\\ \Leftrightarrow {\left( {{a^2} - 2{h^2}} \right)^2} = 0 \Leftrightarrow a = \sqrt 2 h \Leftrightarrow h = \frac{a}{{\sqrt 2 }}\end{array}\)
Tam giác ABC đều cạnh \(a \Rightarrow {S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{2} \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = \frac{a}{{\sqrt 2 }}.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 6 }}{4}\).
Chọn A.