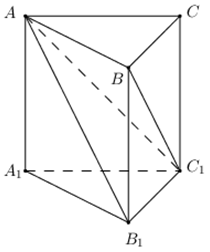
Câu hỏi
Cho lăng trụ \(ABC{A_1}{B_1}{C_1}\) có diện tích mặt bên \(AB{B_1}{A_1}\) bằng \(4\), khoảng cách giữa cạnh \(C{C_1}\) và mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng 6. Tính thể tích khối lăng trụ \(ABC{A_1}{B_1}{C_1}\)
- A \(24\)
- B \(18\)
- C \(12\)
- D \(9\)
Phương pháp giải:
+) Chứng minh \(d\left( {C{C_1};\left( {AB{B_1}{A_1}} \right)} \right) = d\left( {{C_1};\left( {AB{B_1}{A_1}} \right)} \right)\), từ đó tính thể tích của \({C_1}.AB{B_1}{A_1}\).
+) So sánh thể tích \({C_1}.AB{B_1}{A_1}\) với thể tích lăng trụ từ đó tính thể tích lăng trụ.
Lời giải chi tiết:
Ta có
\(C{C_1}//A{A_1} \Rightarrow C{C_1}//\left( {AB{B_1}{A_1}} \right) \Rightarrow d\left( {C{C_1};\left( {AB{B_1}{A_1}} \right)} \right) = d\left( {{C_1};\left( {AB{B_1}{A_1}} \right)} \right)\)
\( \Rightarrow {V_{{C_1}.AB{B_1}{A_1}}} = \frac{1}{3}d\left( {{C_1};\left( {AB{B_1}{A_1}} \right)} \right).{S_{AB{B_1}{A_1}}} = \frac{1}{3}.6.4 = 8\)
Ta có: \({V_{{C_1}.ABC}} = \frac{1}{3}{V_{ABC.{A_1}{B_1}{C_1}}} \Rightarrow {V_{{C_1}.AB{B_1}{A_1}}} = \frac{2}{3}{V_{ABC.{A_1}{B_1}{C_1}}}\)
\( \Rightarrow {V_{ABC.{A_1}{B_1}{C_1}}} = \frac{3}{2}{V_{{C_1}.AB{B_1}{A_1}}} = \frac{3}{2}.8 = 12\)
Chọn C.