Phương pháp giải:

Vẽ đồ thị hàm số \(y = \left| {\frac{{x + 1}}{{x - 3}}} \right|\) và kết luận.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).

Xét hàm số \(y = \frac{{x + 1}}{{x - 3}}\) có \(y' = \frac{{ - 4}}{{{{\left( {x - 3} \right)}^2}}} < 0\,\,\forall x \in D\).

Đồ thị hàm số \(y = \left| {\frac{{x + 1}}{{x - 3}}} \right|\) được vẽ như sau :

+) Bẽ đồ thị hàm số \(y = \frac{{x + 1}}{{x - 3}}\).

+) Lấy đối xứng toàn bộ phần đồ thị nằm dưới trục Ox qua trục Ox.

+) Xóa đi phần đồ thị phía dưới trục Ox.

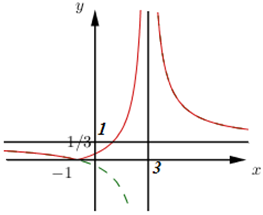
Do đó ta vẽ được đồ thị hàm số \(y = \left| {\frac{{x + 1}}{{x - 3}}} \right|\) như sau :

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có 2 đường tiệm cận là \(x = 3\) và \(y =  - 1\).

Đồ thị \(\left( C \right)\) cắt đường tiệm cận ngang của nó tại 1 điểm.

Hàm số đồng biến trên \(\left( {1;2} \right)\) và hàm số có một điểm cực trị \(x =  - 1\).

Vậy khẳng định sai là đáp án C.

Chọn C.