Câu hỏi
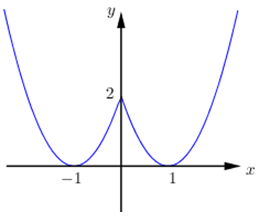
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới đây:
Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\)
(II). Hàm số đồng biến trên khoảng \(\left( { - 1;2} \right)\)
(III).Hàm số có ba điểm cực trị
(IV). Hàm số có giá trị lớn nhất bằng 2.
Số mệnh đề đúng trong các mệnh đề trên là:
- A \(4\)
- B \(2\)
- C \(4\)
- D \(1\)
Phương pháp giải:
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu, các điểm cực trị và GTLN, GTNN của hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy hàm số đã cho
+) Đồng biến trên \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
+) Hàm số có 3 điểm cực trị.
+) Hàm số không có GTLN.
Do đó các mệnh đề (I), (III) đúng.
Chọn B.
Câu hỏi trước
