Câu hỏi
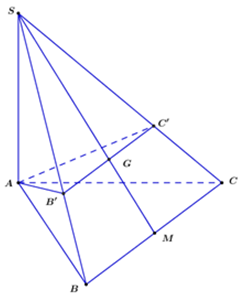
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông cân ở \(B\) , \(AC = a\sqrt {2.} \) \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và \(SA = a.\) Gọi \(G\) là trọng tâm của tam giác \(SBC\) Một mặt phẳng đi qua hai điểm \(A,G\) và song song với \(BC\) cắt \(SB,\,SC\) lần lượt tại \(B'\) và \(C'\) . Thể tích khối chóp \(S.AB'C'\)bằng:
- A \(\frac{{2{a^3}}}{9}\)
- B \(\frac{{2{a^3}}}{{27}}\)
- C \(\frac{{{a^3}}}{9}\)
- D \(\frac{{4{a^3}}}{{27}}\)
Phương pháp giải:
+) Xác định các điểm \(B',\;C'.\)
+) Sử dụng định lý Ta-lét tính các tỉ số \(\frac{{SB'}}{{SB}},\;\;\frac{{SC'}}{{SC}}.\)
+) Sử dụng công thức tính tỉ lệ thể tích: Cho các điểm \(M \in SA,\;\;N \in SB,\;\;P \in SC\) ta có: \(\frac{{{V_{SMNP}}}}{{{V_{SABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}}.\)
+) Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \frac{1}{3}Sh.\)
Lời giải chi tiết:
Qua G, kẻ đường thẳng song song với BC, cắt SC tại B’ và cắt SC tại C’.
Gọi M là trung điểm của BC.
\( \Rightarrow \frac{{SG}}{{SM}} = \frac{2}{3}\) (tính chất đường trung tuyến).
Ta có: \(B'C'//BC \Rightarrow \frac{{SB'}}{{SB}} = \frac{{SC'}}{{SC}} = \frac{{SG}}{{SM}} = \frac{2}{3}\) (định lý Ta-let)
\(AB = \frac{{AC}}{{\sqrt 2 }} = a\;(\Delta ABC\) cân tại \(B)\)
Có: \({V_{SABC}} = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}SA.\frac{1}{2}A{B^2} = \frac{1}{3}.a.\frac{1}{2}.{a^2} = \frac{1}{6}{a^3}.\)
Theo công thức tỉ lệ thể tích ta có:
\(\frac{{{V_{SAB'C'}}}}{{{V_{SABC}}}} = \frac{{SA}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{2}{3}.\frac{2}{3} = \frac{4}{9} \Rightarrow {V_{SAB'C'}} = \frac{4}{9}{V_{SABC}} = \frac{4}{9}.\frac{1}{6}{a^3} = \frac{2}{{27}}{a^3}.\)
Chọn B.