Câu hỏi
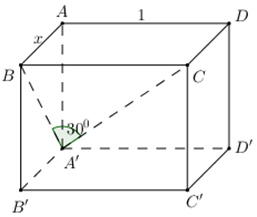
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = x,\,AD = 1.\) Biết rằng góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABB'A'} \right)\) bằng \({30^0}.\) Tìm giá trị lớn nhất \({V_{\max }}\) của thể tích khối hộp \(ABCD.A'B'C'D'\)
- A \({V_{\max }} = \frac{{\sqrt 3 }}{4}\)
- B \({V_{\max }} = \frac{1}{2}\)
- C \({V_{\max }} = \frac{3}{2}\)
- D \({V_{\max }} = \frac{{3\sqrt 3 }}{4}\)
Phương pháp giải:
+) Xác định góc giữa A’C và (ABB’A’).
+) Sử dụng định lí Pytago tính AA’.
+) Sử dụng công thức tính thể tích \({V_{ABC.A'B'C'}} = AA'.AB.AD = V\). Áp dụng BĐT Cô-si tìm Vmax.
Lời giải chi tiết:
Ta có \(BC \bot \left( {ABB'A'} \right) \Rightarrow A'B\) là hình chiếu của \(A'C\) lên \(\left( {ABB'A'} \right)\)
\( \Leftrightarrow \angle \left( {A'C;\left( {ABB'A'} \right)} \right) = \angle \left( {A'C;A'B} \right) = \angle BA'C = {30^0}\).
\(BC \bot \left( {ABB'A'} \right) \Rightarrow BC \bot A'B \Rightarrow \Delta A'BC\) vuông tại A’.
Xét tamg giác vuông A’BC có : \(A'B = BC.\cot {30^0} = \sqrt 3 \)
Xét tam giác vuông AA’B có : \(AA' = \sqrt {A'{B^2} - A{B^2}} = \sqrt {3 - {x^2}} \)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.AB.AD = \sqrt {3 - {x^2}} .x = V\)
Áp dụng BĐT Cô-si ta có \(\sqrt {3 - {x^2}} .x \le \frac{{3 - {x^2} + {x^2}}}{2} = \frac{3}{2} \Rightarrow {V_{\max }} = \frac{3}{2} \Leftrightarrow 3 - {x^2} = {x^2} \Leftrightarrow x = \frac{{\sqrt 6 }}{2}\).
Chọn C.