Phương pháp giải:

+ Dựa vào mối quan hệ về khoảng cách \(d\left( {a;b} \right) = d\left( {a;\left( P \right)} \right) = d\left( {N;\left( P \right)} \right) = d\left( {M;\left( P \right)} \right) = MH\)

Với \(b \subset \left( P \right)//a;\,M;N \in a;\,MH \bot \left( P \right)\)

+ Ta dựng hình bình hành \(ABCD\), gọi \(O\) là chân đường cao hạ từ \(S\) xuống đáy.

+ Xác định \(d\left( {A;\left( {SBC} \right)} \right) = d\left( {N;\left( {SBC} \right)} \right)\) với \(N \in AD\) được chọn phù hợp

và \(d\left( {SA;BC} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {H;\left( {SAD} \right)} \right)\)  với \(H \in BC\)  được chọn phù hợp

+ Dựa vào tam giác đồng dạng để tính \(SO\), từ đó tính thể tích khối chóp \(V = \dfrac{1}{3}h.S\) với \(h\) là chiều cao hình chóp và \(S\) là diện tích đáy.

Lời giải chi tiết:

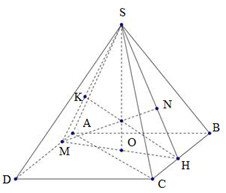
Dựng hình bình hành \(ABCD\).

Gọi O là chân đường vuông góc kẻ từ S đến mặt phẳng \(\left( {ABCD} \right)\) \(\left( {O \in \left( {ABCD} \right)} \right)\)

Qua điểm O kẻ đường thẳng vuông góc với BC cắt BC và AD lần lượt tại H và K.

Khi đó ta có \(HM \bot BC;\,HM \bot AD;\,SO \bot BC;SO \bot AD\) (do \(SO \bot \left( {ABCD} \right)\))

 suy ra \(BC \bot \left( {SHM} \right);AD \bot \left( {SHM} \right)\)

Trong \(\left( {SHM} \right)\) kẻ \(MN \bot SH\) tại \(N\) và \(HK \bot SM\) tại \(K.\)

Ta có \(MN \bot SH\) và \(MN \bot BC\) (do \(BC \bot \left( {SHM} \right)\)) nên \(MN \bot \left( {SBC} \right)\) tại \(N \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = MN\)

Vì \(AD//BC \Rightarrow AD//\left( {SBC} \right);\,M \in AD \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right) = MN = \dfrac{{a\sqrt {15} }}{5}\)

Tương tự ta có \(HK \bot \left( {SAD} \right)\) tại \(K \Rightarrow d\left( {H;\left( {SAD} \right)} \right) = HK\)

Vì \(BC//AD \Rightarrow BC//\left( {SAD} \right);H \in BC \Rightarrow d\left( {BC;SA} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {H;\left( {SAD} \right)} \right) = HK = \dfrac{{a\sqrt {15} }}{5}\)

Xét tam giác \(SHM\) có hai đường cao bằng nhau \(MN = HK\) nên tam giác \(SHM\) cân tại S. Lại có \(SO \bot MN \Rightarrow O\) là trung điểm của \(MN.\)

Ta có \({S_{ABCD}} = MH.BC = 2{S_{ABC}} \Leftrightarrow MH.a = 2.\dfrac{{{a^2}\sqrt 3 }}{4} \Rightarrow MH = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OM = \dfrac{{MH}}{2} = \dfrac{{a\sqrt 3 }}{4}\)

Xét tam giác \(MKH\) vuông tại \(K \Rightarrow MK = \sqrt {M{H^2} - H{K^2}}  = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{15{a^2}}}{{25}}}  = \dfrac{{a\sqrt 3 }}{{2\sqrt 5 }}\)

Ta có \(\Delta MKH\) dồng dạng với \(\Delta MOS\)(g-g) nên \(\dfrac{{KH}}{{SO}} = \dfrac{{MK}}{{MO}} \Rightarrow SO = \dfrac{{MO.HK}}{{MK}} = \dfrac{{\dfrac{{a\sqrt 3 }}{4}.\dfrac{{a\sqrt {15} }}{5}}}{{\dfrac{{a\sqrt 3 }}{{2\sqrt 5 }}}} = \dfrac{{a\sqrt 3 }}{2}\)

Khi đó thể tích \({V_{S.ABC}} = \dfrac{1}{3}.SO.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{8}\) 

Chọn B.